Large spectral partitions

In this numerical study we search for partitions minimizing the sum of their first Dirichlet Laplacian eigenvalues. What I propose is a trick which allows us to study partitions with large cell numbers with low computational cost. We recall that an initial study for large partitions was made by Bourdin, Bucur and Oudet here. Their computation for 512 cells was made using a super computer at the Texas Advanced Computing Center. The need for such a computer was justified by the fact that even when looking at a small cell they still used a matrix of the size of the whole domain to compute its eigenvalue.

The idea I propose in the following is to reduce the size of the computation matrix when the cells have emerged. Instead of using the whole grid to compute the eigenvalue, we could restrict our attention to a rectangular neighborhood of the cell and use finite differences on that smaller grid in order to compute its eigenvalue. This has an effect on the computational accuracy, since we do not search for information about the eigenvalues of a cell when we are far away from that cell. There is also a huge speed improvement, since the size of the computation matrix is equal to the number of points in the computation grid. Thus, with this improvement it is possible to perform the computation for 512 cells on a $512 \times 512$ grid on a laptop computer in a reasonable amount of time. The computation for $512$ cells took about $5$ hours, while for small cell numbers a few minutes suffice. In order to save time we initially use a coarse grid until the cells emerge from the random initial data. Then we interpolate the data on a refined grid and re-optimize.

Below you can see some computations on various domains, with various numbers of cells.

$31$ cells $37$ cells $37$ cells
$45$ cells $120$ cells $512$ cells
Below you can see an optimization example on the sphere, with a similar algorithm. Instead on computing the eigenvalues on the whole triangulation, we find a neighborhood of each cell and use only those values for the eigenvalue computation. This allows us to work with up to $40000$ points on the sphere, while working with the whole domain took days of computatioin time only for $10000$ points. This new formulations performs in about $10$ minutes on a regular computer for the case of $32$ cells presented below.
In the following you can see some examples of computations for large numbers of cells on some 3D surfaces like the sphere a torus and a different surface (taken from the article of Elliott and Ranner). In general we see that for large number of cells we have many hexagons, which is natural in any configuration where we only have triple points. In the case of the sphere we note that we obtain $12$ pentagons and $n-12$ hexagons, while in the case of the torus we also have some heptagons in the configuration.
$72$ cells $90$ cells $120$ cells
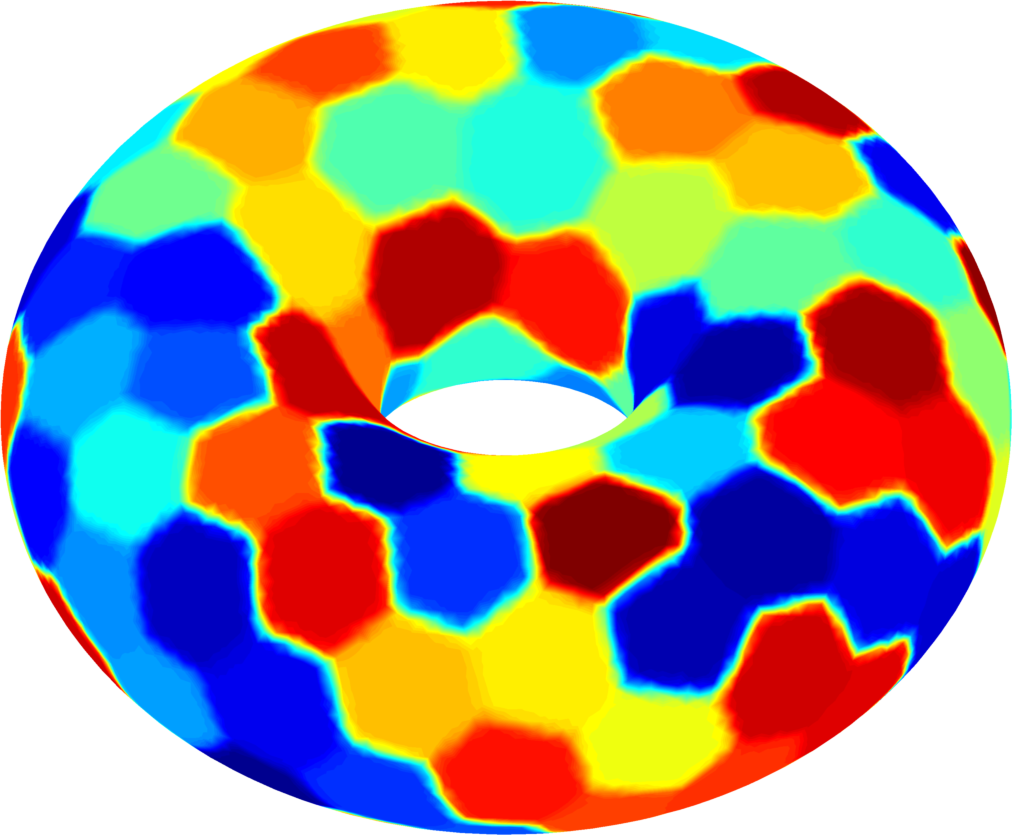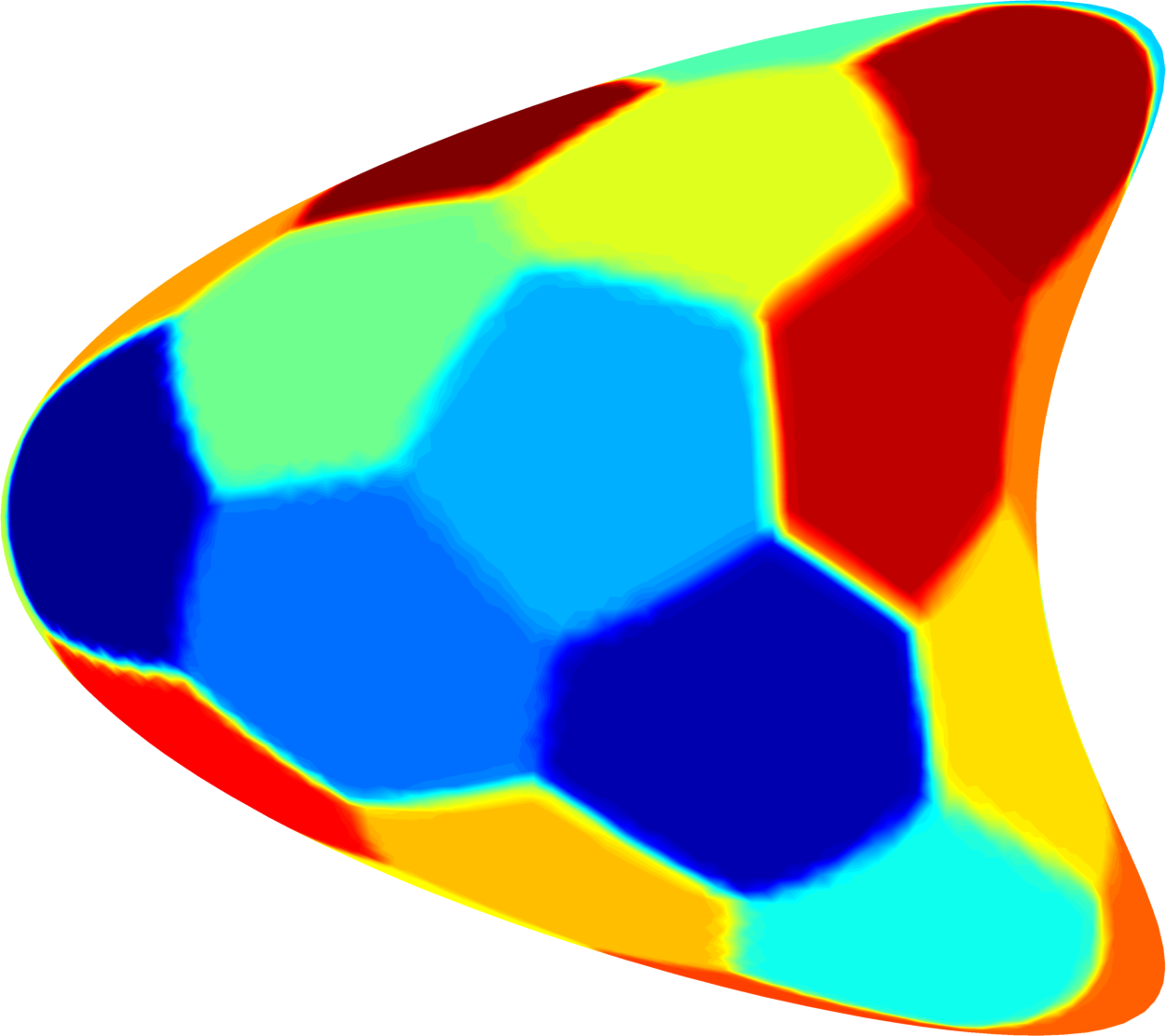
$32$ cells $64$ cells $128$ cells
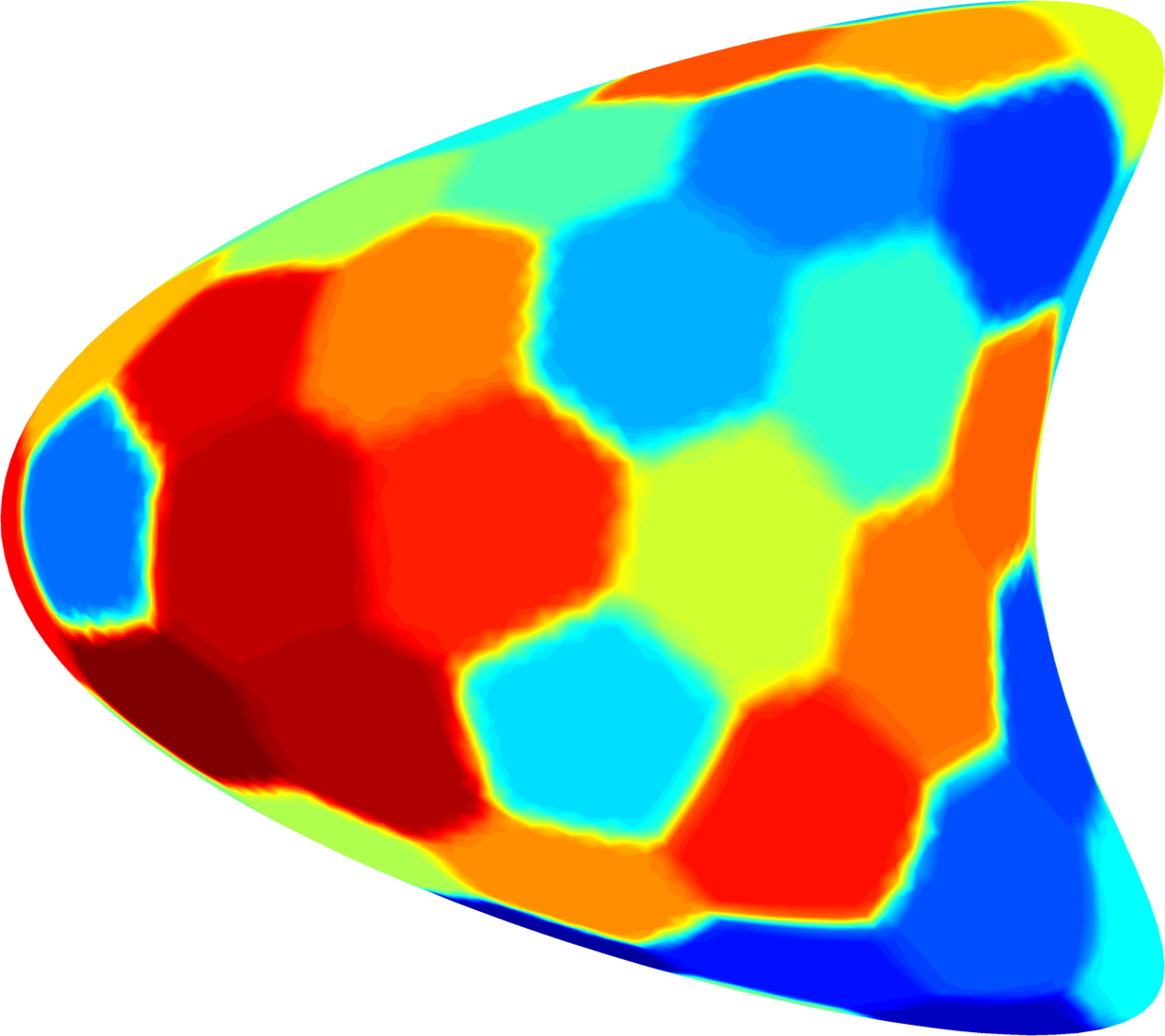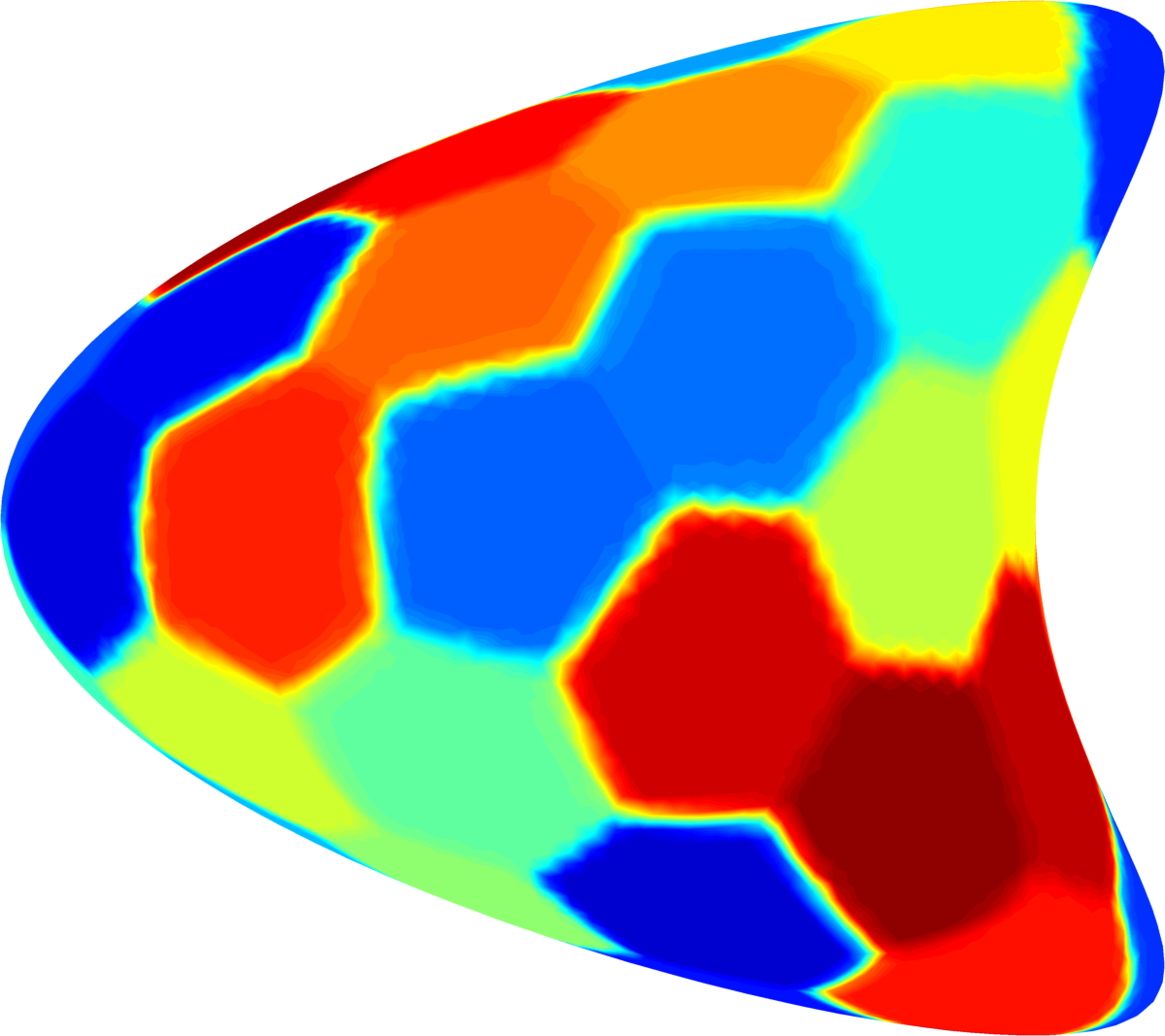
$32$ cells $48$ cells $64$ cells

Created: Feb 2016