J'enseigne des maths à l'
Ecole polytechnique et je
cherche à établir des
résultats
en probabilités dans l'équipe
PEIPS
au
CMAP
et m'intéresse principalement
à des questions issues des sciences du vivant (biologie ou
écologie).
Par exemple :
Quel est l'impact de la variabilité de l'environnement sur
la croissance ou la survie d'une population ?
Lorsqu'un parasite se multiplie à l'intérieur de
cellules qui se divisent, comment
la répartition des parasites et le temps de division de la cellule
affectent sa propagation dans l'oganisme ?
Comment la compétition régule-t-elle de grandes populations ?
A quelle vitesse se propage une épidémie sur un graphe de populations ?
Combien y-a-t-il de caribous ?
Thèmes d'intérêt
Probabilités : Processus de branchement, Processus
de Markov branchant, Environnement aléatoire, Processus de Naissance et
mort,
Equations Différentielles Stochastiques, Descente de
l'infini, Systèmes dynamiques, Processus de Lévy, Graphes aléatoires ...
Ecologie: Environnement variable en temps ou en
espace, Dynamique des populations, Abondance
d'espèces, Réponses fonctionnelles.
Biologie: Division, infection et contamination cellulaire.
Epidémie sur un graphe et métapopulations.
Coordonnées
Adresse
: CMAP, Ecole Polytechnique, Route de
Saclay
91128 Palaiseau
Cedex, FRANCE. |
|
|
| E-mail
: vincent.bansaye'chez'polytechnique.edu |
|
| Téléphone
: 01 69 33 45 67 |
|
| Bureau
: 00 30 25, 2ème étage, aile 0. |
|
|
Pour etre sur une liste de diffusion ou proposer un
exposé, n'hésitez pas à nous écrire ....
Vie asssociative : lien vers l'Association Paestel; lien vers le collectif Massy Ambition Education.
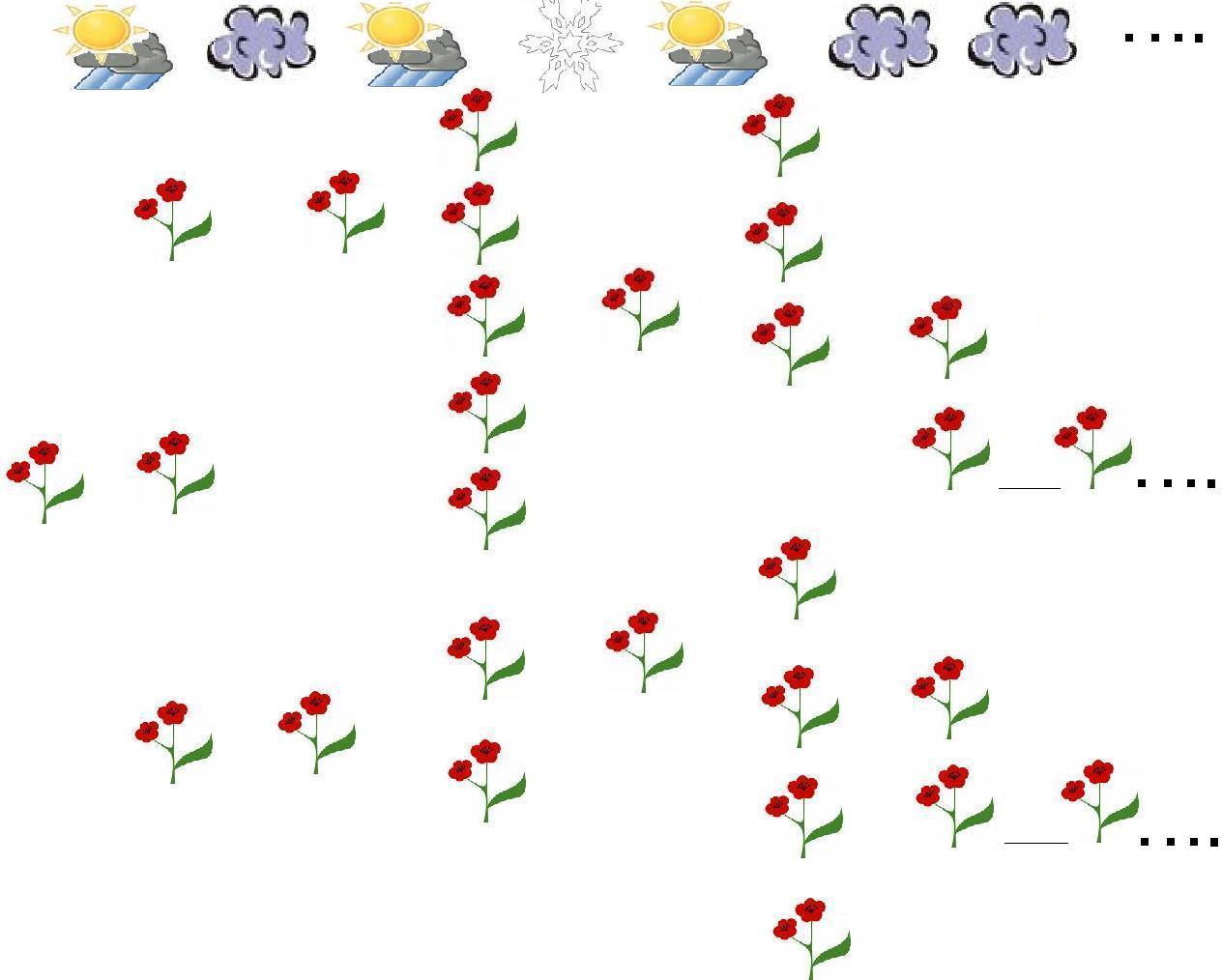
Une animation pour les processus de branchement en environnement
aléatoire
(à environnement donné,
les fleurs
se reproduisent indépendamment les unes des
autres
suivant une même loi).
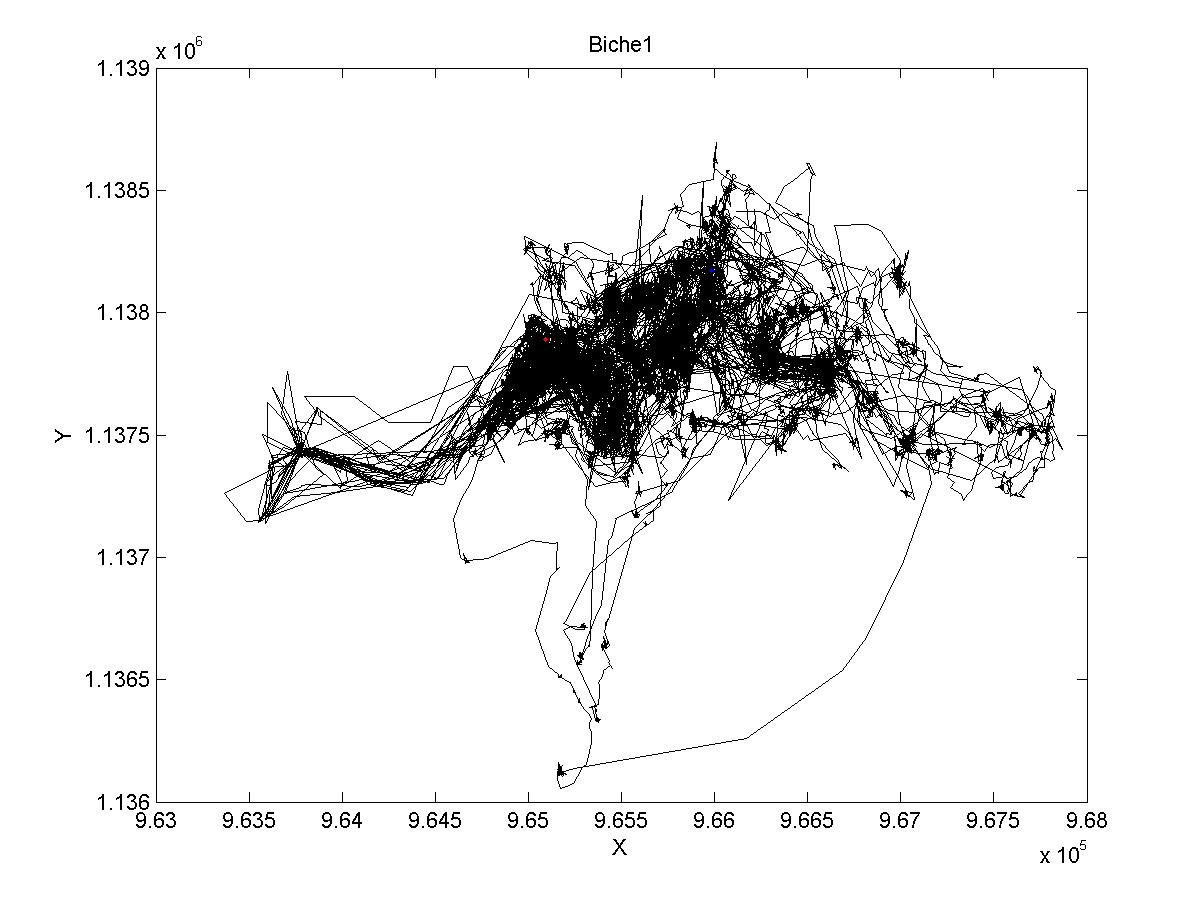
Une trajectoire de biche :
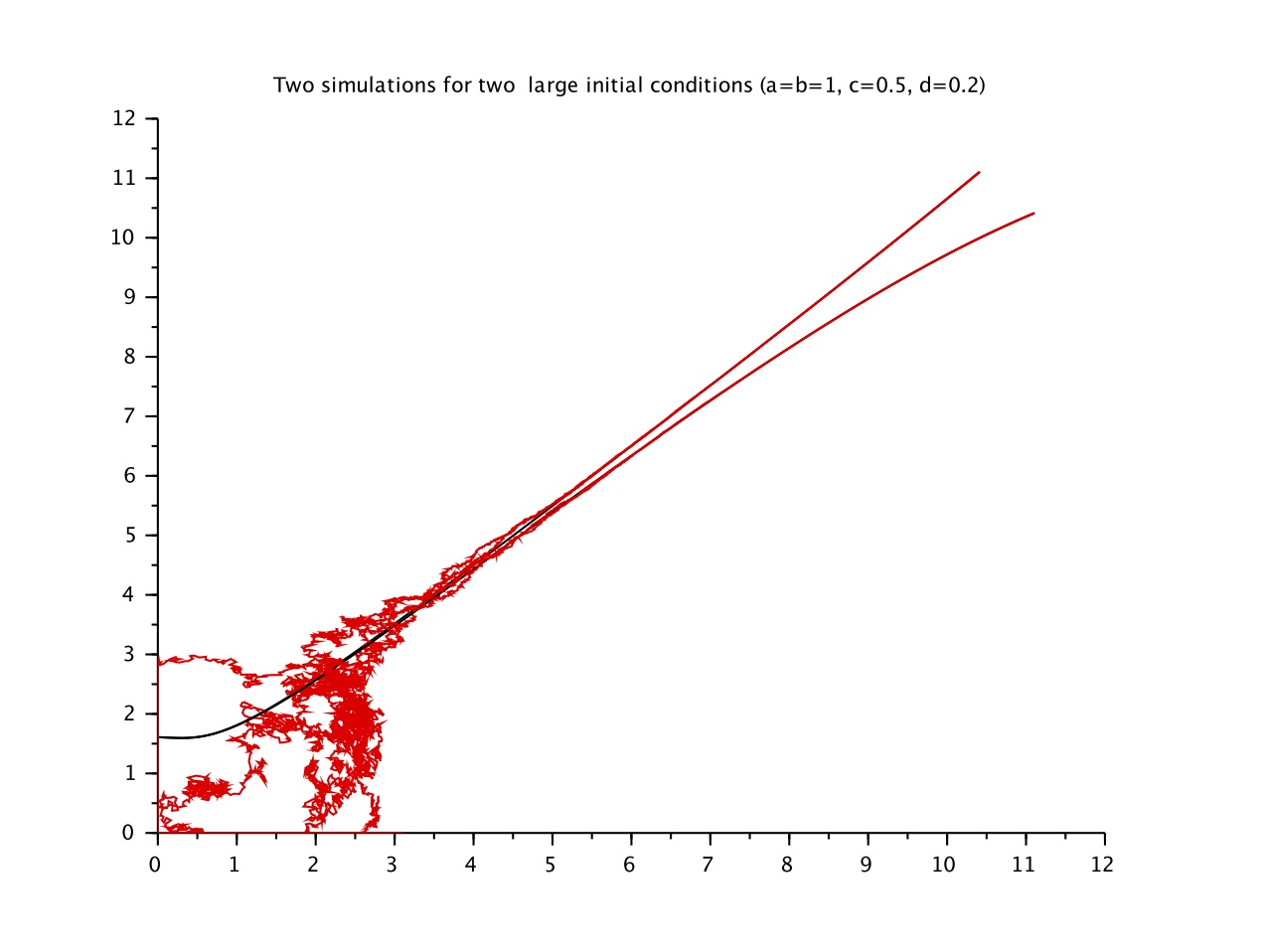
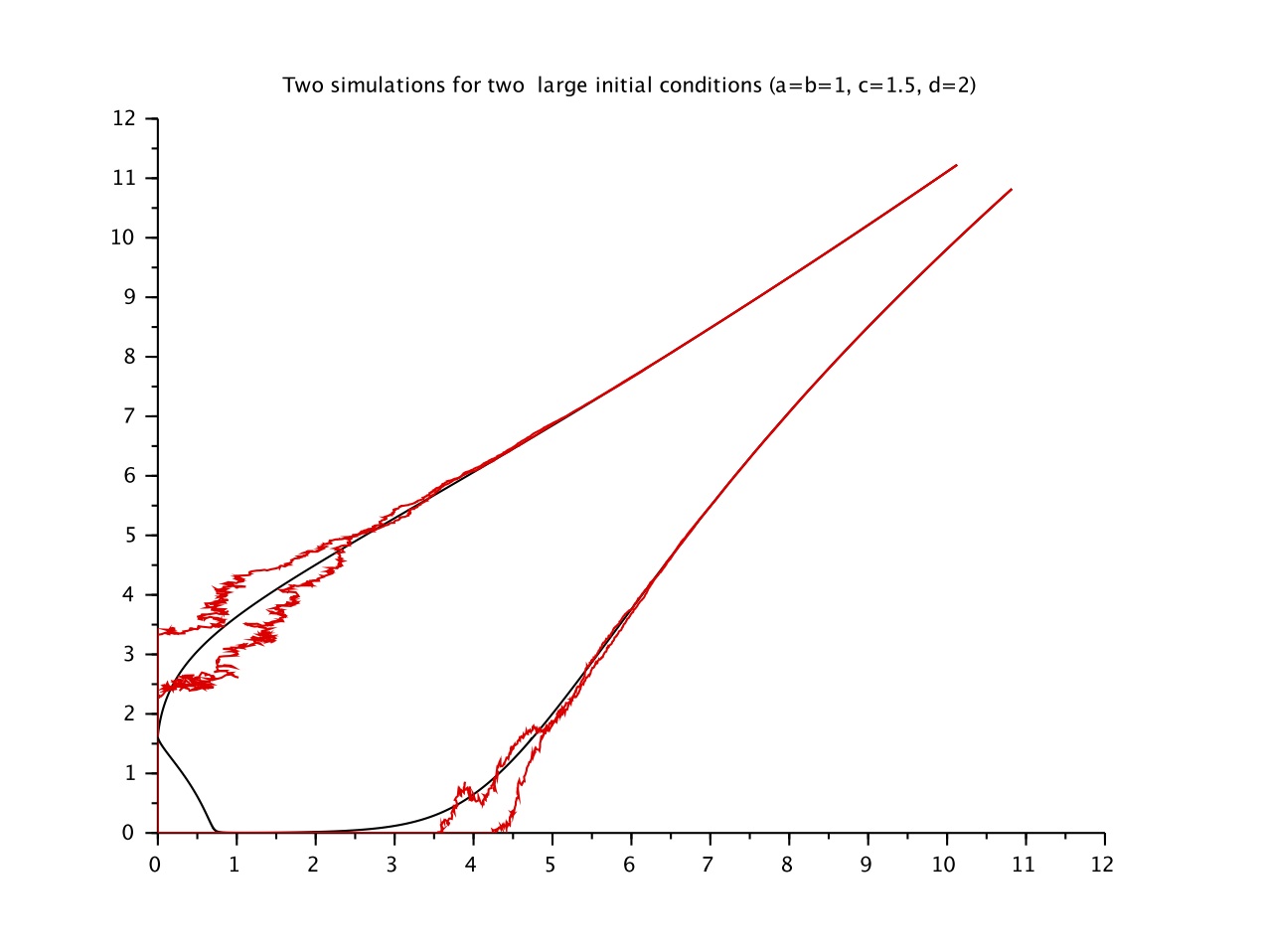
Descente de l'infini pour des
modèles stochastiques compétitifs type Lotka Volterra