Longest minimal length partitions

This page is related to the following paper written in collaboration with Edouard Oudet. This work was motivated by the following article on the CNRS Images des Mathematiques website. This note mentions an article that shows that in dimension two the convex shape that maximizes the length of an area bisecting curve is the disk. Many questions can be asked regarding this problem:

In the meantime Frank Morgan contacted us, indicating that this problems dates to some older post on his blog from 2010. In 2017 a nice paper was published which sloves the problem in dimension two for small areas. The following paper solves the conjecture in dimension two for domains symmetric with respect to both coordinate axes and perturbations of the disk

First, let's recall that given a Lipschitz open domain with finite volume $\Omega \subset \Bbb{R}^d$ with $|\Omega|=v_d$ and $c \in (0,1)$ there exist subsets $\omega \subset \Omega$ with volume $|\omega|=c|\Omega|$ such that the relative perimeter $\operatorname{Per}_\Omega(\omega)$ is minimal. Denote by $L(\Omega,c)$ the minimal perimeter obtained for one of these sets. It turns out that there exist convex sets $\Omega$ with fixed volume such that $L(\Omega,c)$ is maxima. The objective of this work is to investigate numerically how the optimal shape $\Omega$ changes for $c\in (0,1)$.

An analogue problem can be formulated in the case of minimal length partition. For $n\geq 2$ and $c_i>0$ with $\sum_{i=1}^n c_i=1$, it is possible to find partitions $(\omega_i)$ of $\Omega$ that verify the volume constraints $|\omega_i|=c_i|\Omega|$ and have a minimal total relative perimeter. Again, the problem of maximizing this minimal relative perimeter of a partition makes sense, since in the paper we prove that a maximizing set exists among covnex sets.

The numerical approximation of minimal perimeter partitions is done using a $\Gamma$-convergence relaxation of the perimeter based on the Modica-Mortola theorem. You can check out what I wrote on this page. In the paper we describe how to implement this using the Finite Elements method. Once the optimal partition is computed, we find a perturbation of the domain increasing the minimal relative perimeter using techniques based on the shape derivative concept.

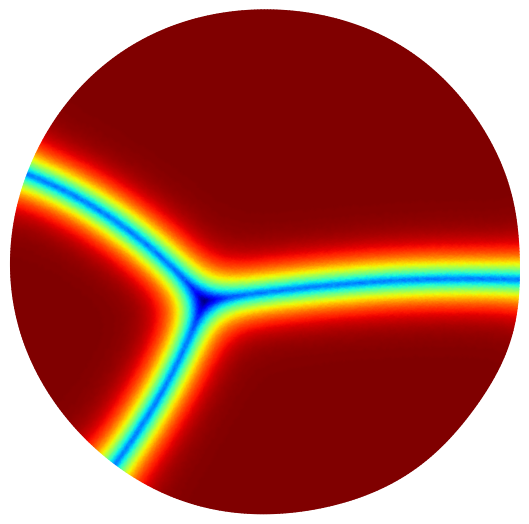
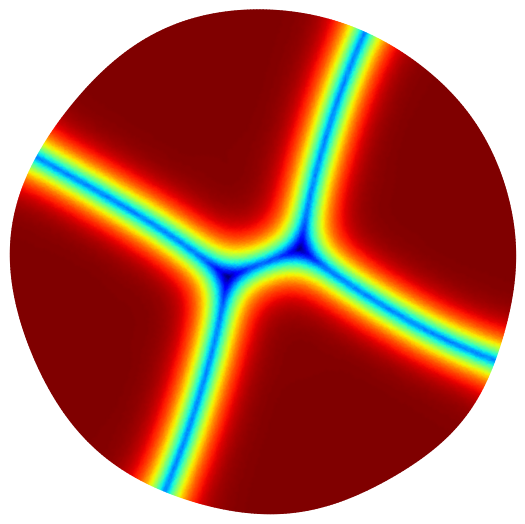
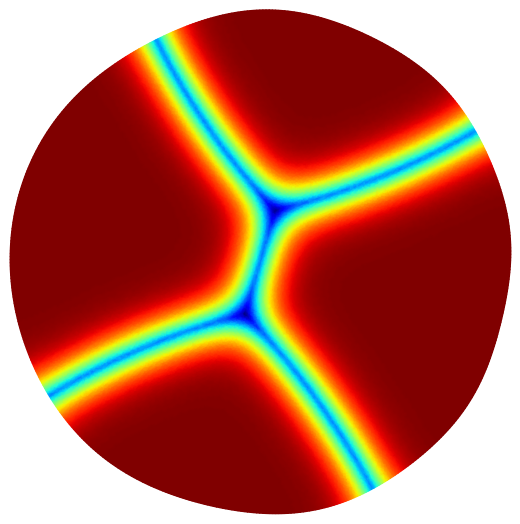
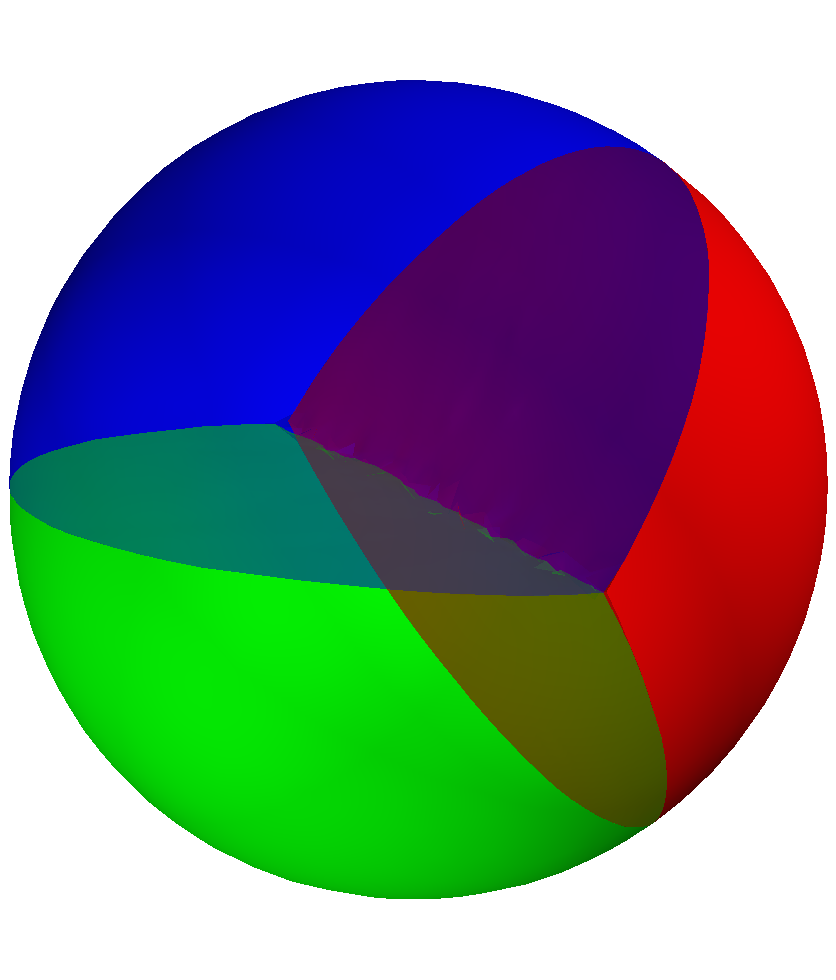
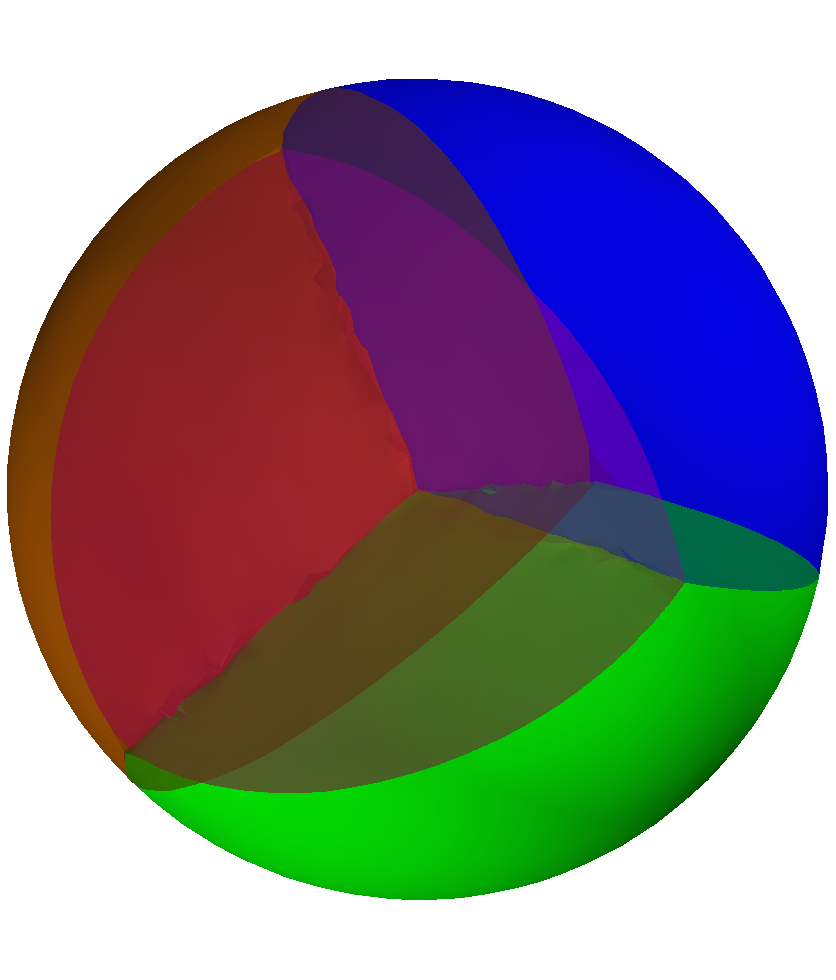
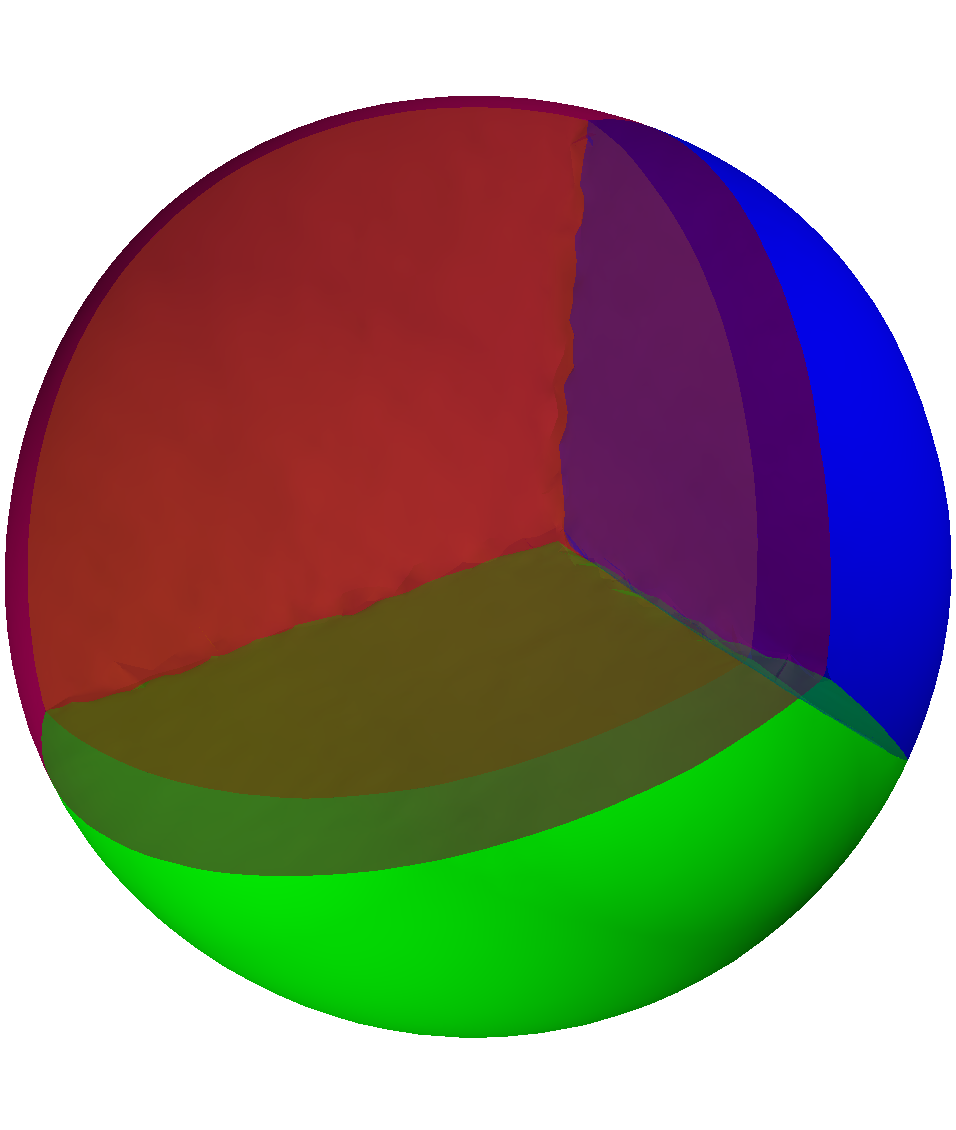
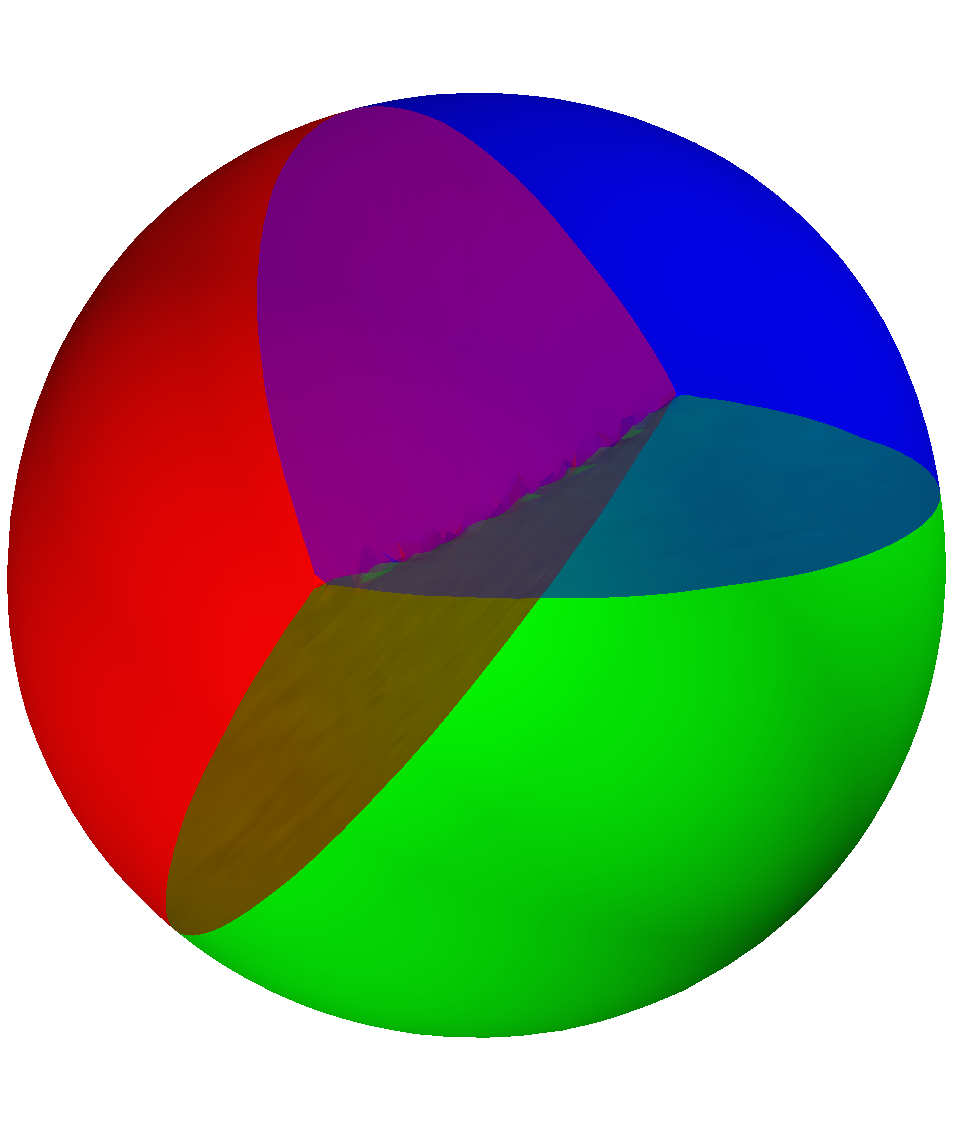
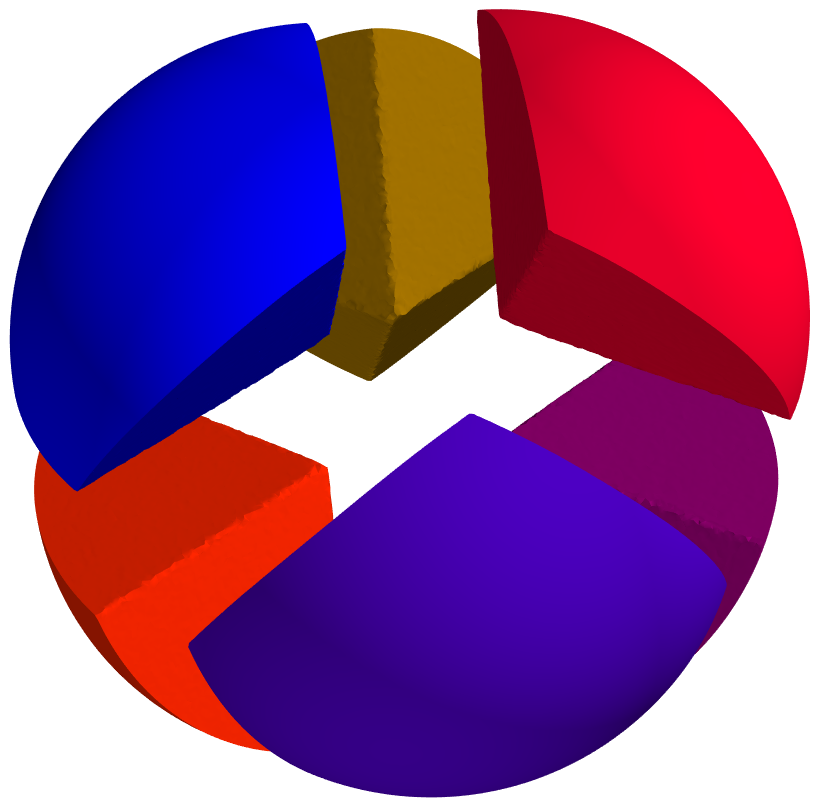
The numerical results of our paper suggest that the disk is indeed minimizer when maximizing the minimal relative perimeter with respect to any volume ratio $c \in (0,1)$. Moreover, this results seems to extend in dimension three and to the case of minimal length partitions. Below you can find some illustration of the maximizing sets we obtained together with the associated minimal relative perimeter sets and partitions. For more information regarding the optimization algorithms and the interpretation of the results, see the contents of the article.

Examples of codes used in our article can be found in the following Github repository.

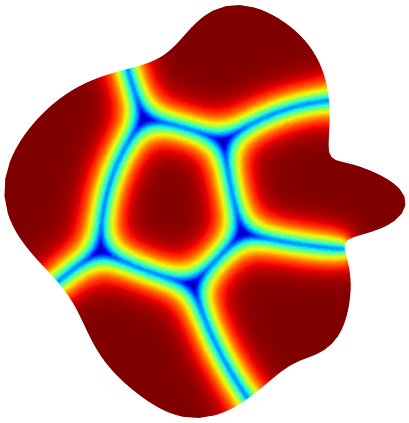
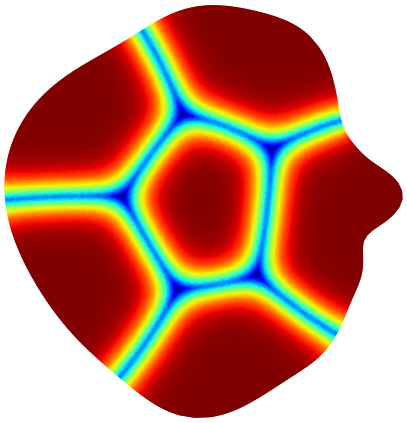
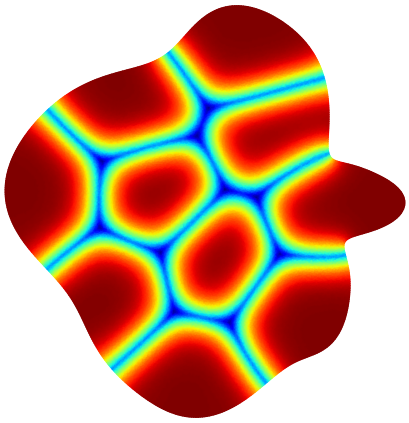
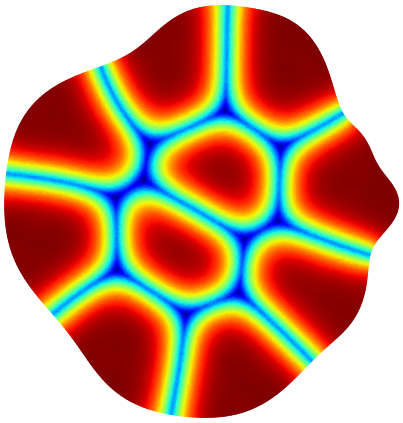
Below you can see illustrations of the gradient flow algorithm for maximizing the minimal relative perimeter of a partition. The cost function for the Modica-Mortola functional at the current iteration is shown.

Iter 1: 3.314 Iter 6: 3.381 Iter 13: 3.391 Iter 20: 3.426 Iter 70: 3.446 Iter 150: 3.451
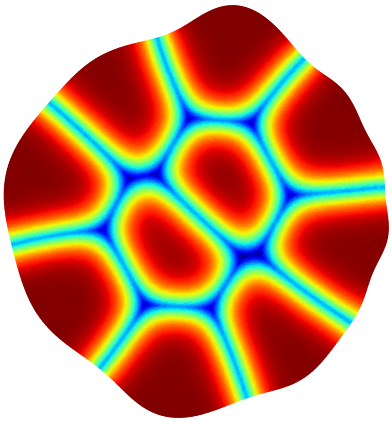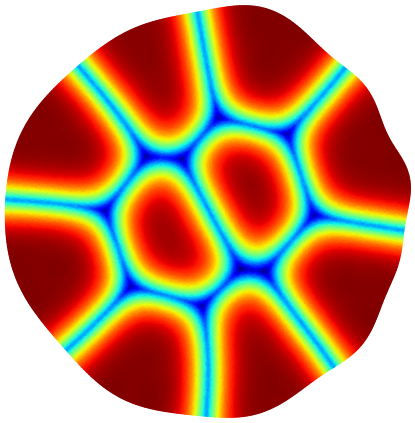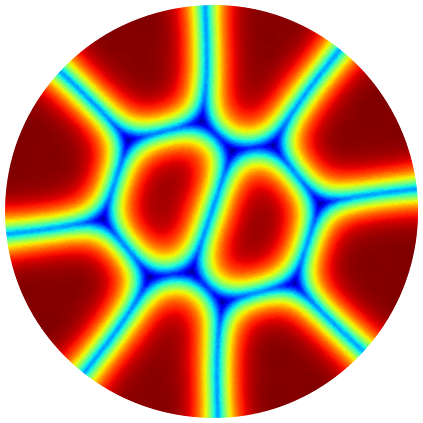Iter 1: 4.663 Iter 6: 4.795 Iter 13: 4.794 Iter 20: 4.863 Iter 70: 4.892 Iter 150: 4.902

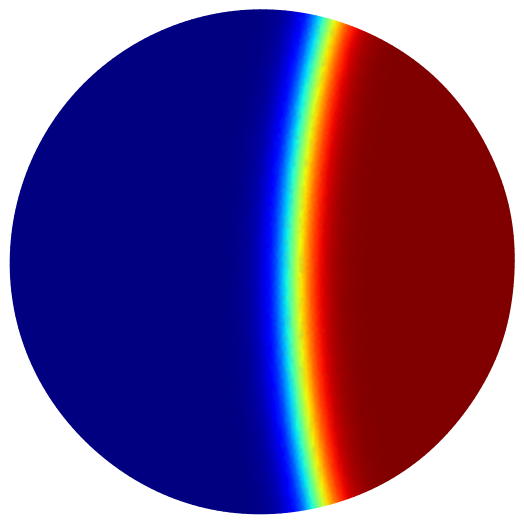
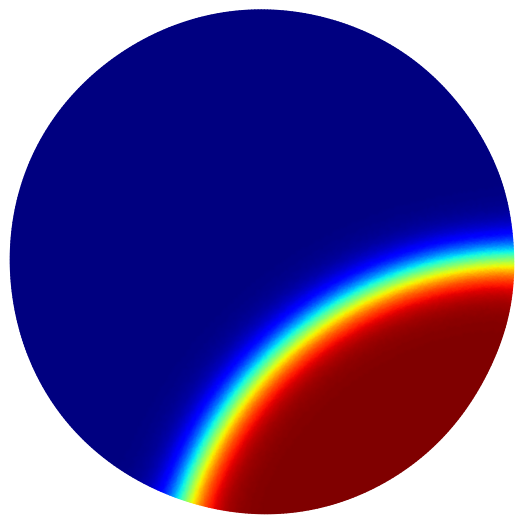
Here are some maximization results for the minimal perimeter of one phase and different volume ratios. The final result is always the disk or the ball.

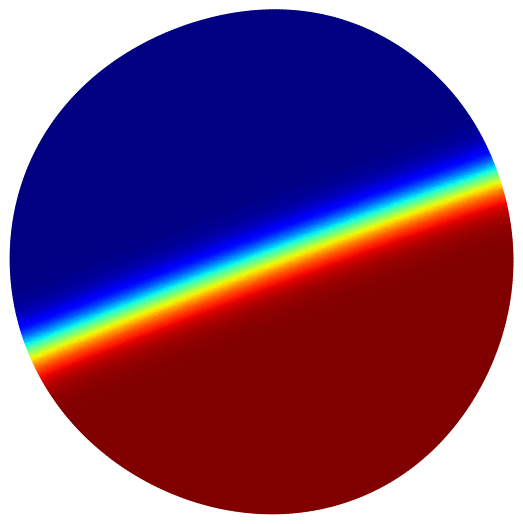Vol frac=0.5 Vol frac=0.4 Vol frac=0.25
Vol frac=0.25 Vol frac=0.5 Vol frac=0.4

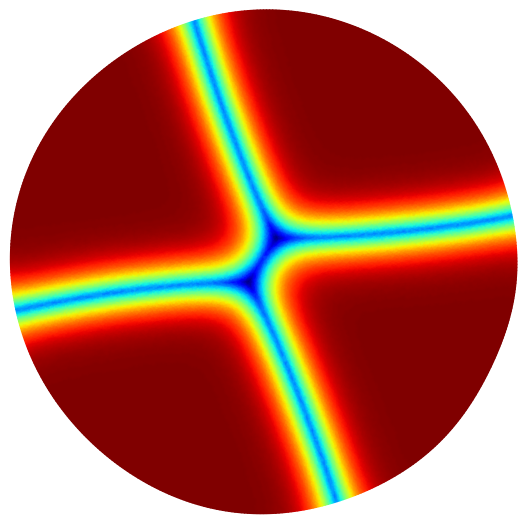
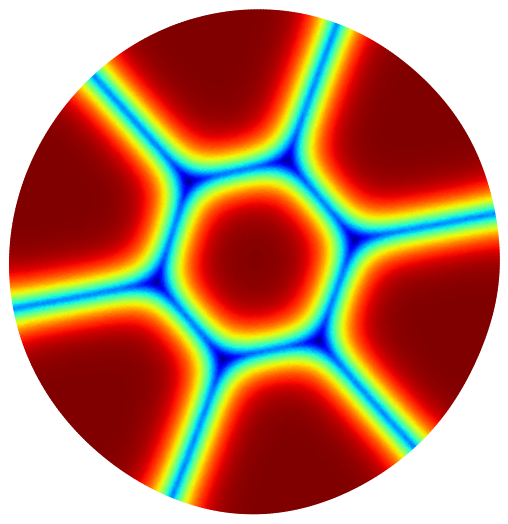
Below are some maximization results for the case of partitions into equal or non-equal volumes. In this case also, the final result is always the disk or the ball.

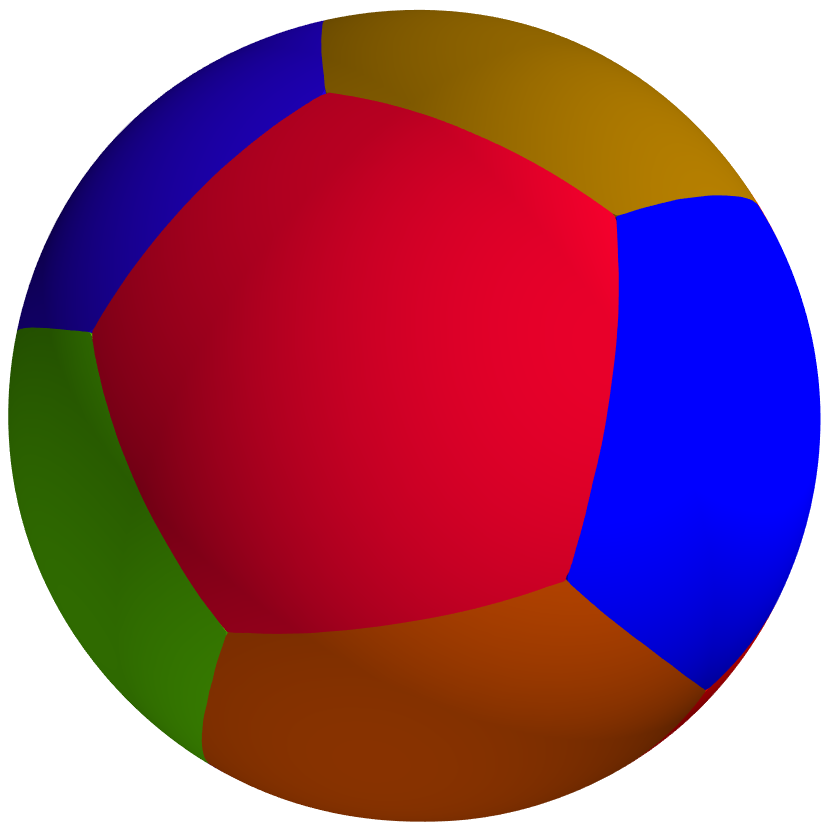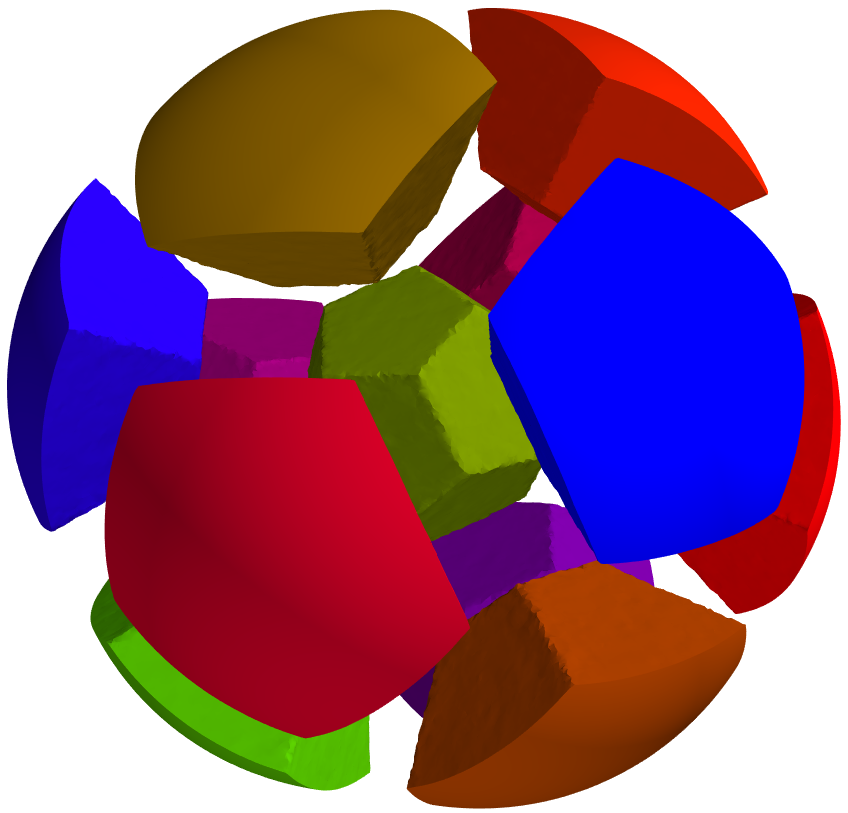Similar results hold when maximizing the minimal geodesic perimeter of a partition under surface-area constraints.

Created: Feb 2021