Spectral optimal partitions on surfaces
This is a continuation of the numerical study presented here.
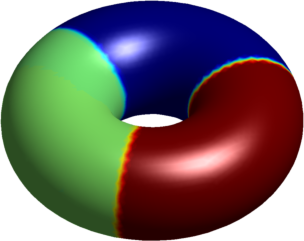
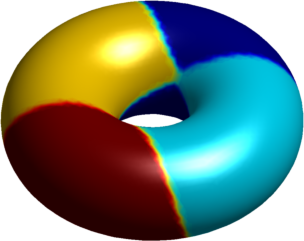
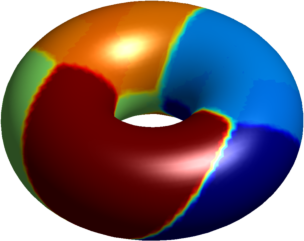
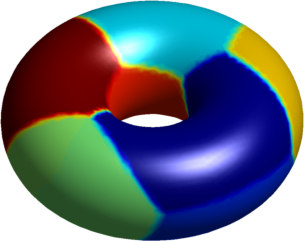
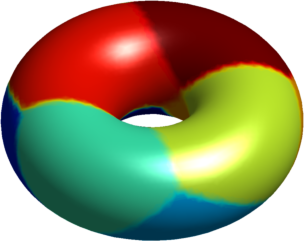
The numerical results presented below concern the problem partitioning a surface into pieces such that the sum of the first Laplace-Beltrami eigenvalues of the parts is minimized. We consider the problem $$ \min \sum_{i=1}^n \lambda_1^{LB}(S_i)$$ where $(S_i)$ is a partition of a manifold into $n$ parts. The same problem was studied recently by Elliott and Ranner (link), using a different numerical method.
A fictious domain method is used, in order to detect the structure of the partition (inspired from the 2D computations made by Bourdin, Bucur, Oudet - link)
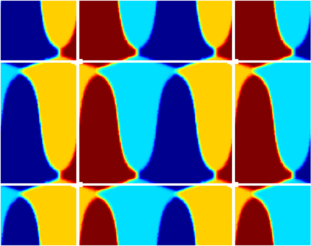
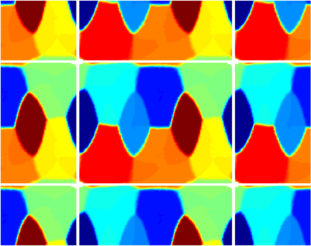
The computations presented below were made using Matlab, and the visualization was made in Matlab. The first set of pictures represent the results on a torus together with the corresponding two dimensional flattenings (the central rectangle represents the torus, while the periodic continuations are shown to give a clearer perspective on the structure of the optimal partition.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
The last pictures concern a more complex surface: the Banchoff-Chmutov surface of order $4$.
 |
 |
 |
Created: Sept 2015