A $\Gamma$- convergence method for optimal partitions on manifolds

in collaboration with Edouard Oudet

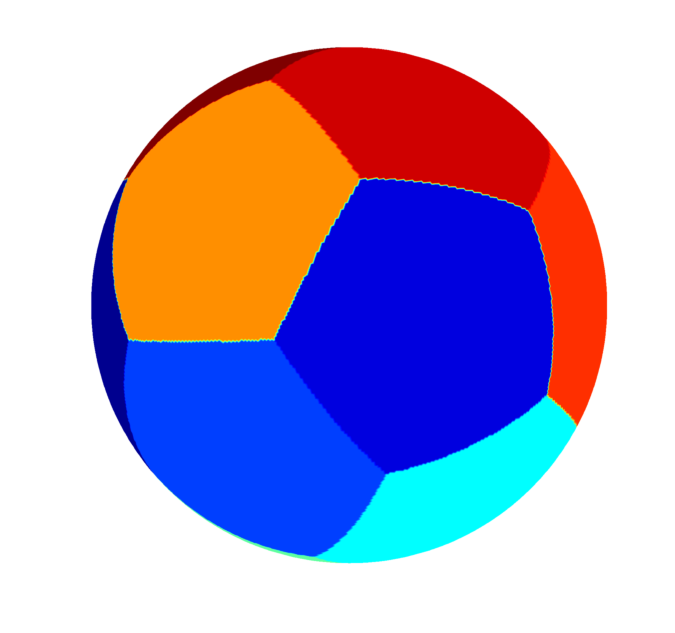
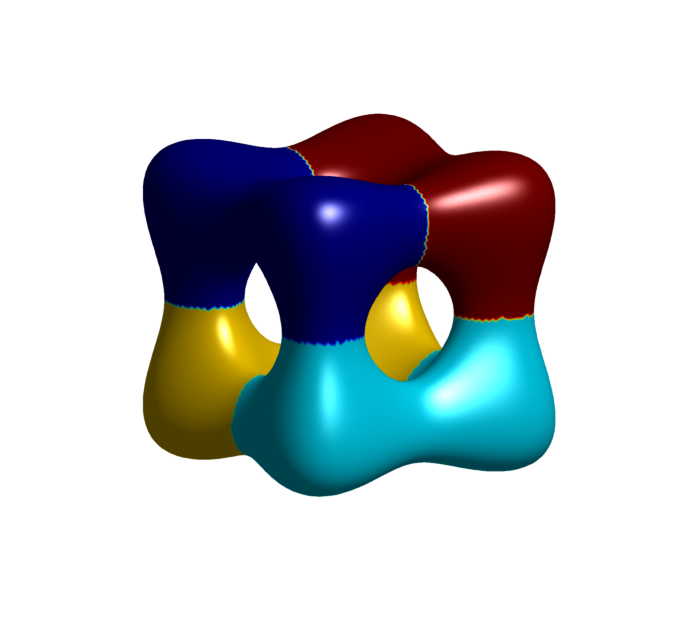
(Work in progress) Using an approximation of the perimeter on the sphere, we compute numerically the partitions into sets of equal area which minimize the sum of the perimeters.

Hold your mouse over the picture to see an animated view (it may take a while to load).

$12$-sets partition

$32$-sets partition
The method works on arbitrary surfaces in three dimensions. Below you can see optimal perimeter minimizing partitions for the case of the Bonchoff-Chmutov surface of order $4$, which is the zero level set of the function $f(x,y,z)=T_4(x)+T_4(y)+T_4(z)$, where $T_4 = 8X^4-8X^2+1$ is the fourth order Chebychev polynomial of the first kind.

$4$-sets partition

$8$-sets partition
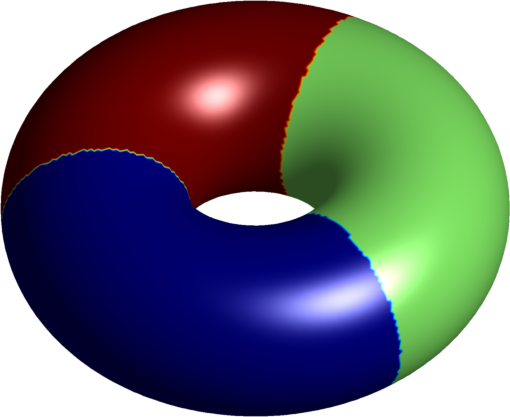
Below are some numerical results concerning the perimeter minimizing partition on the torus with radii $1$ and $0.6$. To have a more precise idea on the topology of the optimal partition, in the right, the two dimensional projection of the partition is presented. The middle rectangle represents the torus, and the periodic continuations are presented for clarity.
$2$ cells partition $2$ cylinders
$3$ cells partition $3$ cylinders
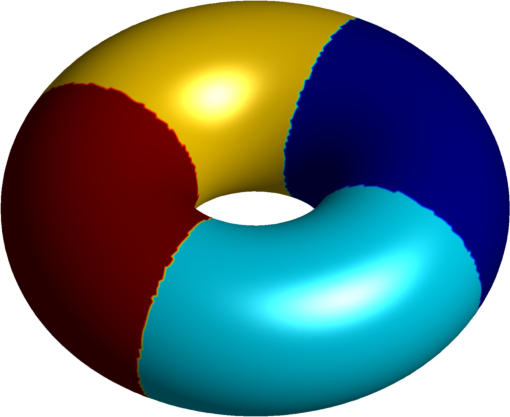
$4$ cells partition $4$ cylinders
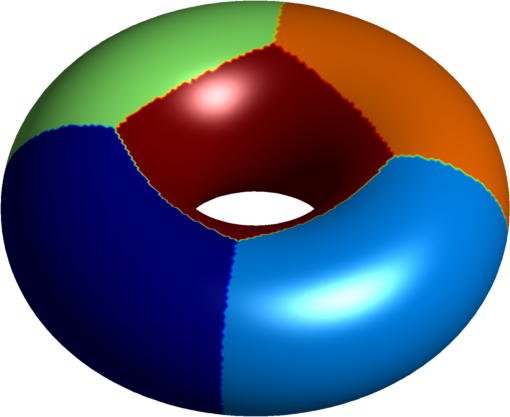$5$ cells partition various polygons
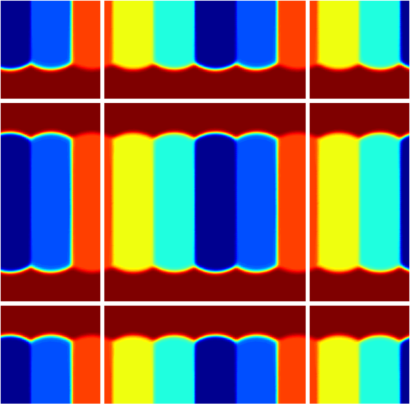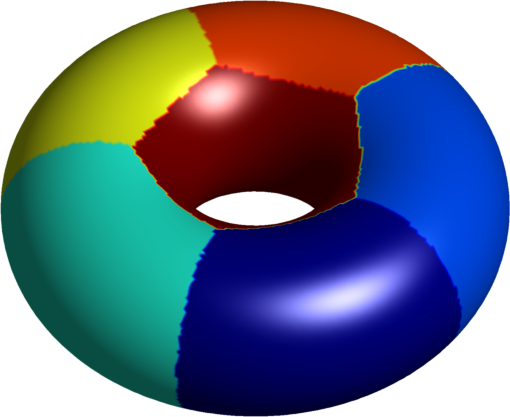
$6$ cells partition various polygons
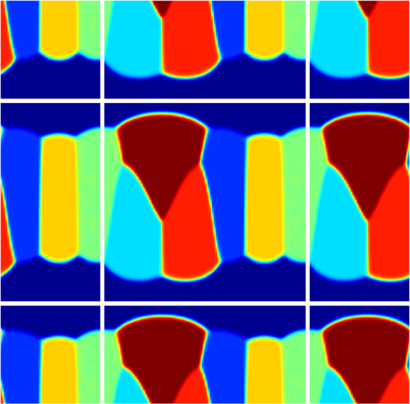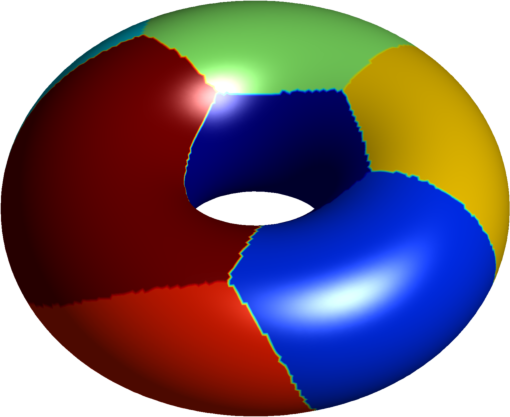
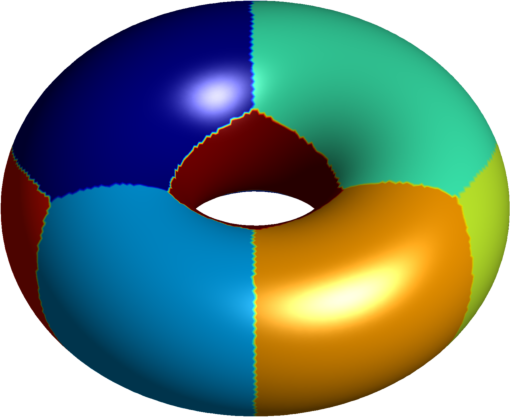
$7$ cells partition various polygons
$8$ cells partition various polygons
$9$ cells partition various polygons
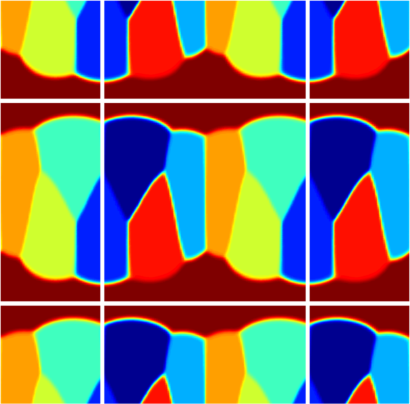
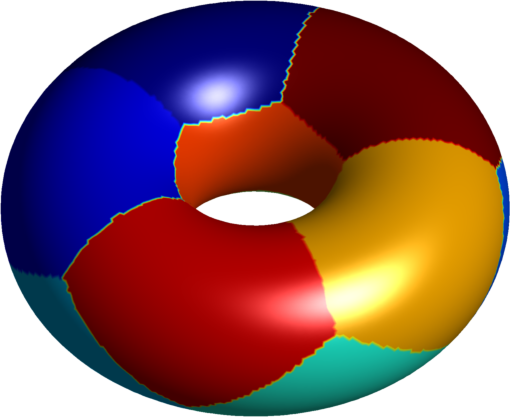
$10$ cells partition various polygons
$11$ cells partition various polygons
$13$ cells partition various polygons

Below are a few optimal configurations on a double torus.

$2$ sets partition $4$ sets partition $6$ sets partition

Created: Mar 2015, Last modified: June 2015