Beniamin BOGOSEL

Spectral optimal partitions on some 2D regions

I present here some computations of the optimal partitions $(\Omega_i)$ of a polygonal region $D$ associated to the problem $$\min \lambda_1(\Omega_1)+\lambda_1(\Omega_2)+...+\lambda_1(\Omega_N).$$ This kind of problems were studied numerically in the case of a square region $D$ by D. Bucur, E. Oudet, B. Bourdin (link), for large values of $N$. Similar problems (including the minimization of $\max \lambda_1(\Omega_i)$) were studied by V. Bonnaillie-Noel, B. Helffer, G. Vial in different settings and on different regions $D$ (rectangles, polygons, circle sectors, etc) (link). The case of the circle has been studied by S.-M. Chang, C.-S. Lin, T.-C. Lin, W.-W. Lin.

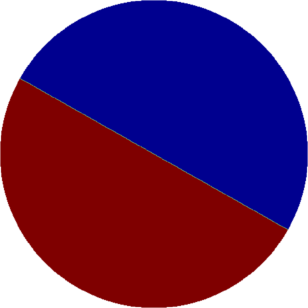
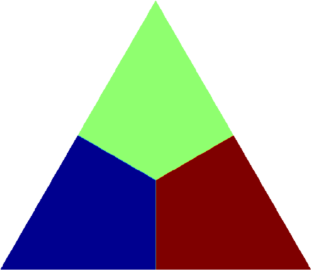
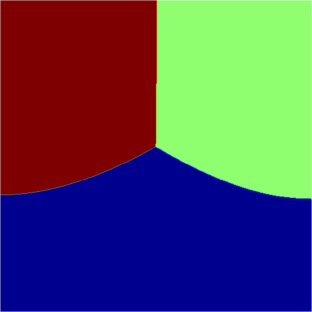
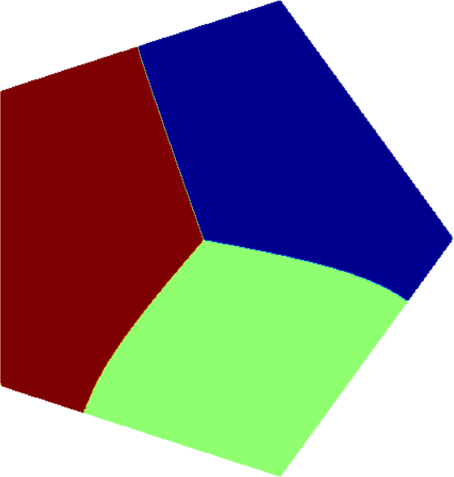
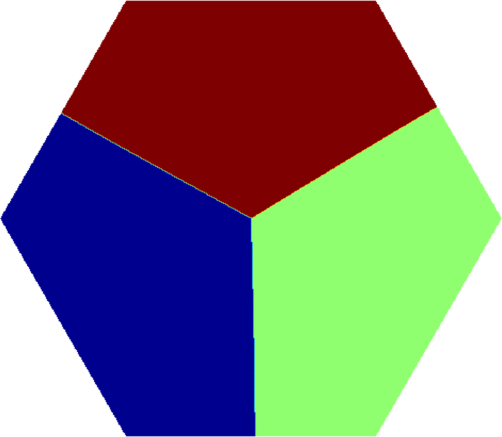
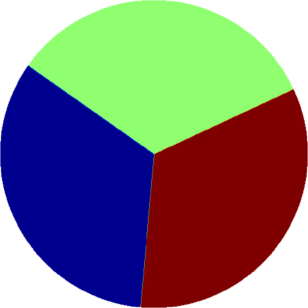
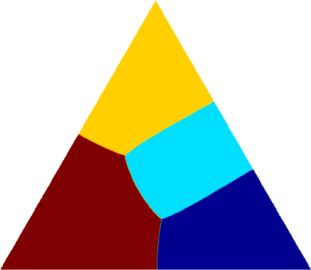
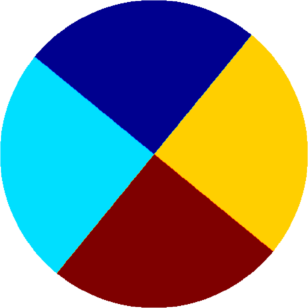
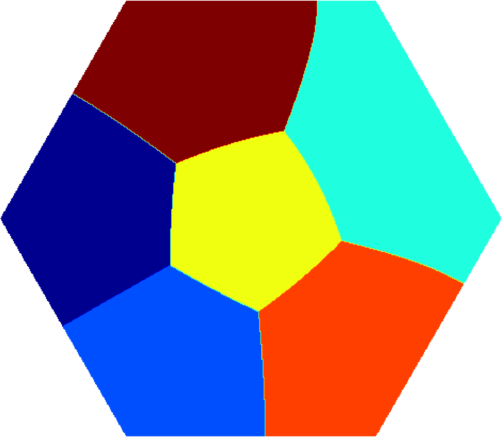
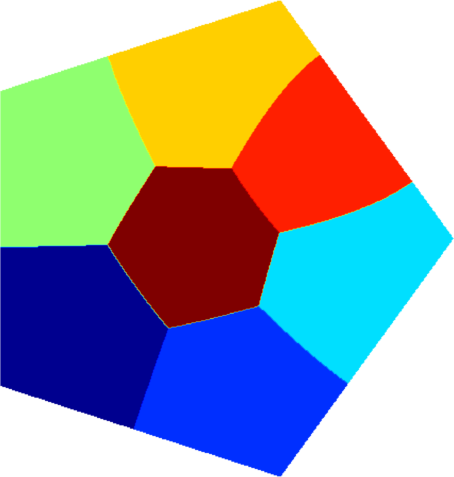
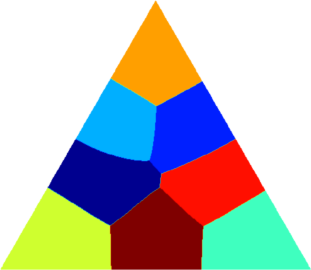
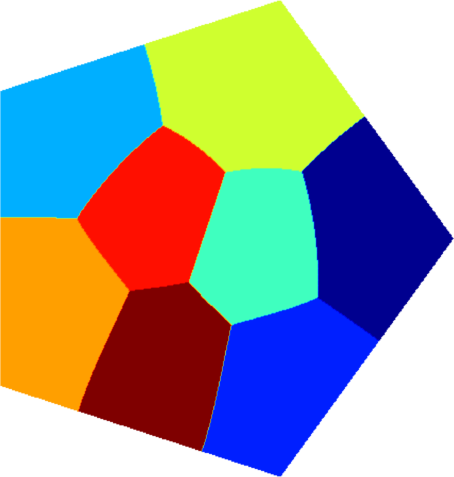
I present below some computations for $2\leq N \leq 10$ in the case where $D$ is an equilateral triangle, a square, a regular pentagon, a regular hexagon, a circle. The computations are mare using a finite element approach: we find a triangulation of the region, write the rigidity and mass matrices, and use a density approach to represent the shapes. The eigenvalues are then computed by reducing the problem to the case of a generalized eigenvalue computation. The approach should work on any domain, although, there is a limit on the number of points we can take in the discretization, since solving large-scale generalized eigenvalue problem can be very slow.

---

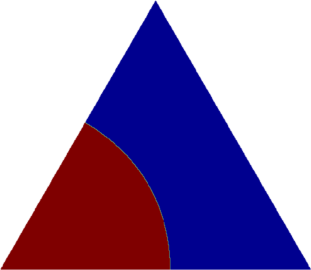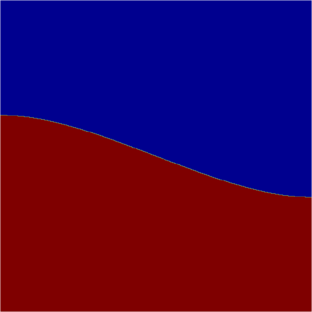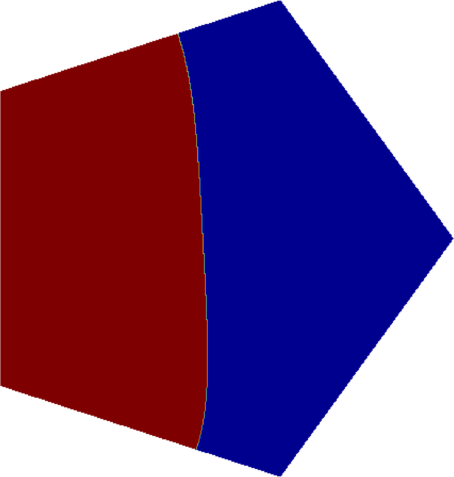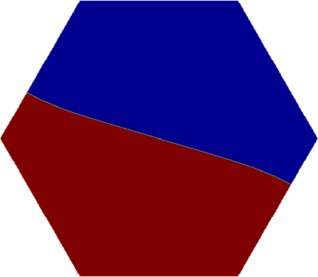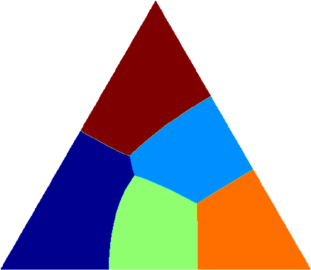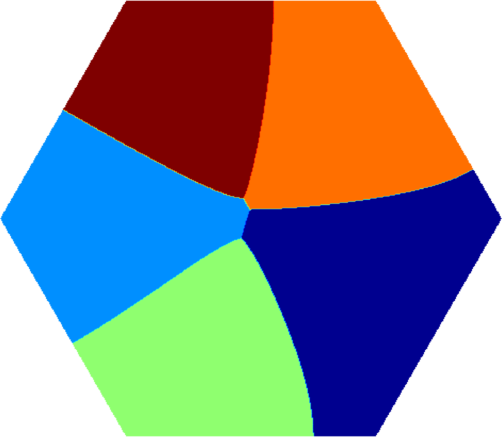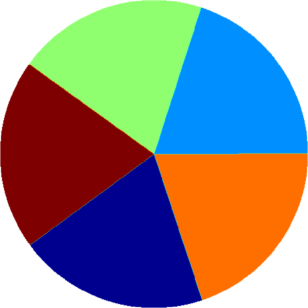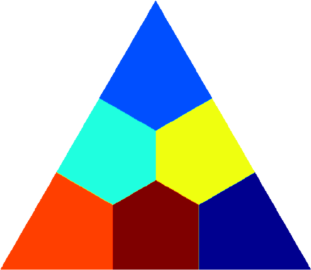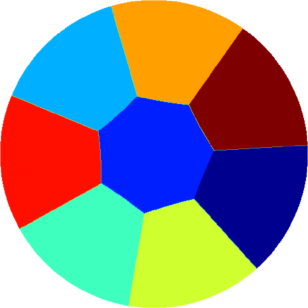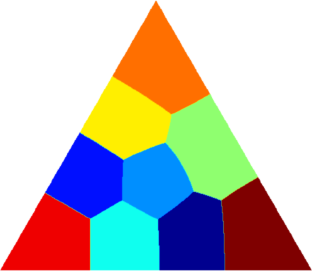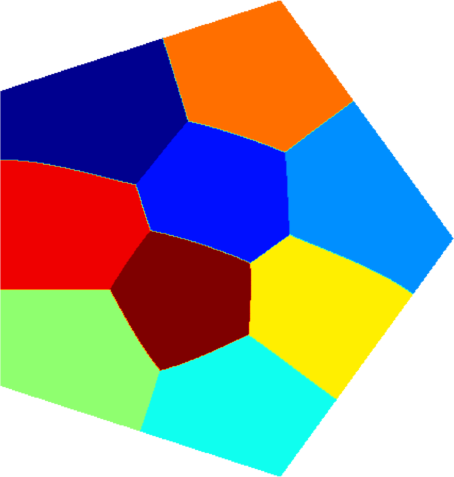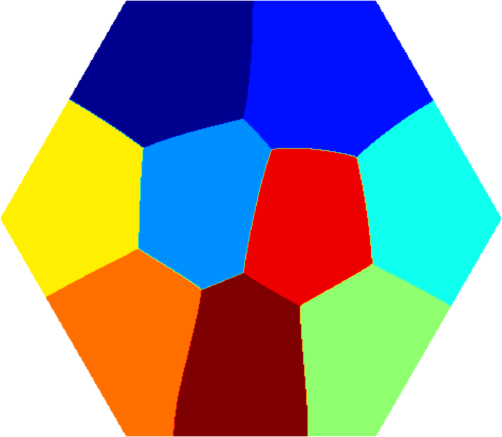Created: Apr 2015