B. Bogosel,
A reverse isoperimetric inequality for convex shapes with inclusion constraint
, 2024
(submitted) (
arxiv:2402.05648)
Abstract
Bibtex
The convex shape contained in a disk having prescribed area and maximal perimeter is completely characterized in terms of the area fraction. The solution is always a polygon having all but one sides equal. The lengths of the sides are characterized through explicit equations. The case of more general containing shapes is also discussed from both theoretical and numerical perspectives.
@misc{bogosel2024reverse,
title={A reverse isoperimetric inequality for convex shapes with inclusion constraint},
author={Beniamin Bogosel},
year={2024},
eprint={2402.05648},
archivePrefix={arXiv},
primaryClass={math.MG}
}
B. Bogosel, A. Henrot, M. Michetti,
Optimization of Neumann eigenvalues under convexity and geometric constraints, 2024
(submitted) (
arxiv:2402.04117)
Abstract
Bibtex
In this paper we study optimization problems for Neumann eigenvalues $\mu_k$ among convex domains with a constraint on the diameter or the perimeter. We work mainly in the plane, though some results are stated in higher dimension. We study the existence of an optimal domain in all considered cases. We also consider the case of the unit disk, giving values of the index $k$ for which it can be or cannot be extremal. We give some numerical examples for small values of $k$ that lead us to state some conjectures.
@misc{bogosel2024optimization,
title={Optimization of Neumann Eigenvalues under convexity and geometric constraints},
author={Beniamin Bogosel and Antoine Henrot and Marco Michetti},
year={2024},
eprint={2402.04117},
archivePrefix={arXiv},
primaryClass={math.AP}
}
S. Amstutz, B. Bogosel,
Nonlocal approximation of the anisotropic perimeter and application to topology optimization, 2023
(submitted) (
hal-04332547)
Abstract
Bibtex
We present a $\Gamma-$convergence approximation of a class of anisotropic perimeter functionals. In contrast to other works on the topic, the construction relies on the solution of possibly nonlinear elliptic boundary value problems. We discuss theoretical and algorithmic aspects. We also show various applications in topology optimization, including multiphase partitioning and overhang penalization in a mechanical framework related to additive manufacturing.
@unpublished{amstutz:hal-04332547,
TITLE = {{Nonlocal approximation of the anisotropic perimeter and application to topology optimization}},
AUTHOR = {Amstutz, Samuel and Bogosel, Beniamin},
URL = {https://hal.science/hal-04332547},
NOTE = {working paper or preprint},
YEAR = {2023},
MONTH = Dec,
KEYWORDS = {Topology optimization ; Additive Manufacturing ; Perimeter},
PDF = {https://hal.science/hal-04332547/file/submission.pdf},
HAL_ID = {hal-04332547},
HAL_VERSION = {v1},
}
B. Bogosel,
Mixed volumes and the Blaschke-Lebesgue theorem, 2023
(accepted in Acta Mathematica Hungarica) (
hal-04306123)
Abstract
Bibtex
The mixed area of a Reuleaux polygon and its symmetric with respect to the origin is expressed in terms of the mixed area of two explicit polygons. This gives a geometric explanation of a classical proof due to Chakerian. Mixed areas and volumes are also used to reformulate the minimization of the volume under constant width constraint as isoperimetric problems. In the two dimensional case, the equivalent formulation is solved, providing another proof of the Blaschke-Lebesgue theorem. In the three dimensional case the proposed relaxed formulation involves the mean width, the area and inclusion constraints.
@unpublished{bogosel:hal-04306123,
TITLE = {{Mixed volumes and the Blaschke-Lebesgue theorem}},
AUTHOR = {Bogosel, Beniamin},
URL = {https://hal.science/hal-04306123},
NOTE = {working paper or preprint},
YEAR = {2023},
MONTH = Nov,
PDF = {https://hal.science/hal-04306123/file/BL2D_Visual.pdf},
HAL_ID = {hal-04306123},
HAL_VERSION = {v1},
}
B. Bogosel,
Volume computation for Meissner polyhedra and applications, 2023
(submitted) (
hal-04258055)
Abstract
Bibtex
The volume of a Meissner polyhedron is computed in terms of the lengths of its dual edges. This allows to reformulate the Meissner conjecture regarding constant width bodies with minimal volume as a series of explicit finite dimensional problems. A direct consequence is the minimality of the volume of Meissner tetrahedras among Meissner pyramids.
@unpublished{bogosel:hal-04258055,
TITLE = {{Volume computation for Meissner polyhedra and applications}},
AUTHOR = {Bogosel, Beniamin},
URL = {https://hal.science/hal-04258055},
NOTE = {working paper or preprint},
YEAR = {2023},
MONTH = Oct,
PDF = {https://hal.science/hal-04258055/file/Volume_Meissner.pdf},
HAL_ID = {hal-04258055},
HAL_VERSION = {v1},
}
B. Bogosel,
A geometric proof of the Blaschke-Lebesgue theorem for the Cheeger constant, 2023
(accepted in Annales de l'Institut Fourier) (
hal-04045140)
Abstract
Bibtex
The first main result presented in the paper shows that the perimeters of inner parallel sets of planar shapes having a given constant width are minimal for the Reuleaux triangles. This implies that the areas of inner parallel sets and, consequently, the inverse of the Cheeger constant are also minimal for the Reuleaux triangles. Proofs use elementary geometry arguments and are based on direct comparisons between general constant width shapes and the Reuleaux triangle.
B. Bogosel, D. Bucur, I. Fragala,
The nonlocal isoperimetric problem for polygons: Hardy-Littlewood and Riesz Inequalities, 2023
(accepted in Mathematische Annalen) (
hal-04001501)
Abstract
Bibtex
Given a non-increasing and radially symmetric kernel in $L ^ 1 _{\rm loc} (\Bbb R ^ 2 ; \Bbb R _+)$, we investigate counterparts of the classical Hardy-Littlewood and Riesz inequalities
when the class of admissible domains is the family of polygons
with given area and $N$ sides. The latter corresponds to study the polygonal isoperimetric problem in nonlocal version. We prove that, for every $N \geq 3$, the regular $N$-gon is optimal for Hardy-Littlewood inequality.
Things go differently for Riesz inequality: while for $N = 3$ and $N = 4$ it is known that the regular triangle and the square are optimal, for $N\geq 5$ we prove that symmetry or symmetry breaking may occur (i.e. the regular $N$-gon may be optimal or not),
depending on the value of $N$ and on the choice of the kernel.
B. Bogosel, G. Buttazzo, E. Oudet,
On the numerical approximation of Blaschke-Santalo diagrams using Centroidal Voronoi Tessellations, 2023
(to appear in ESAIM: Mathematical Modelling and Numerical Analysis) (
hal-03966754)
Abstract
Bibtex
Identifying Blaschke-Santalo diagrams is an important topic that essentially consists in determining the image $Y=F(X)$ of a map $F:X\to\Bbb R^d$, where the dimension of the source space $X$ is much larger than the one of the target space. In some cases, that occur for instance in shape optimization problems, $X$ can even be a subset of an infinite-dimensional space. The usual Monte Carlo method, consisting in randomly choosing a number $N$ of points $x_1,\dots,x_N$ in $X$ and plotting them in the target space $\Bbb R^d$, produces in many cases areas in $Y$ of very high and very low concentration leading to a rather rough numerical identification of the image set. On the contrary, our goal is to choose the points $x_i$ in an appropriate way that produces a uniform distribution in the target space. In this way we may obtain a good representation of the image set $Y$ by a relatively small number $N$ of samples which is very useful when the dimension of the source space $X$ is large (or even infinite) and the evaluation of $F(x_i)$ is costly. Our method consists in a suitable use of Centroidal Voronoi Tessellations which provides efficient numerical results. Simulations for two and three dimensional examples are shown in the paper.
G. Allaire, M. Bihr, B. Bogosel, M. Godoy,
Accessibility constraints in structural optimization via distance
functions, 2022
(accepted in Journal of Computational Physics) (
hal-03864841)
Abstract
Bibtex
This paper is concerned with a geometric constraint, the so-called accessibility constraint,
for shape and topology optimization of structures built by additive manufacturing. The
motivation comes from the use of sacrificial supports to maintain a structure, submitted
to intense thermal residual stresses during its building process. Once the building stage is
finished, the supports are of no more use and should be removed. However, such a removal
can be very difficult or even impossible if the supports are hidden deep inside the complex
geometry of the structure. A rule of thumb for evaluating the ease of support removal is to
ask that the contact zone between the structure and its supports can be accessed from the
exterior by a straight line which does not cross another part of the structure. It mimicks the
possibility to cut the head of the supports attached to the structure with some cutting tool.
The present work gives a new mathematical way to evaluate such an accessibility constraint,
which is based on distance functions, solutions of eikonal equations. The main advantage is
the possibility of computing shape derivatives of such a criterion with respect to both the
structure and the support. We numerically demonstrate in 2D and 3D that, in the context
of the level-set method for topology optimization, such an approach allows us to optimize
simultaneously the mechanical performance of a structure and the accessibility of its building
supports, guaranteeing its additive manufacturing.
@unpublished{allaire:hal-03864841,
TITLE = {{Accessibility constraints in structural optimization via distance functions}},
AUTHOR = {Allaire, Gr{\'e}goire and Bihr, Martin and Bogosel, Beniamin and Godoy, Matias},
URL = {https://hal.archives-ouvertes.fr/hal-03864841},
NOTE = {working paper or preprint},
YEAR = {2022},
MONTH = Nov,
PDF = {https://hal.archives-ouvertes.fr/hal-03864841/file/article_accessibilite_v4.pdf},
HAL_ID = {hal-03864841},
HAL_VERSION = {v1},
}
Pedro R.S. Antunes, B. Bogosel,
Optimization of the Steklov-Lamé eigenvalues with respect to the domain, 2022
(submitted) (
hal-03676230) (
arxiv:2205.11364)
Abstract
Bibtex
This work deals with theoretical and numerical aspects related to the
behavior of the Steklov-Lamé eigenvalues on variable domains. After
establishing the eigenstructure for the disk, we prove that for a certain class of Lamé parameters, the disk maximizes the first non-zero eigenvalue under area or perimeter constraints in dimension two. Upper bounds for these eigenvalues can be found in terms of the scalar Steklov
eigenvalues, involving various geometric quantities. We prove that the
Steklov-Lamé eigenvalues are upper semicontinuous for the complementary Hausdorff convergence of $\varepsilon$-cone domains and, as a consequence,
there exist shapes maximizing these eigenvalues under convexity and volume constraints. A numerical method based on fundamental solutions is proposed for computing the Steklov-Lamé eigenvalues, allowing to study numerically the shapes maximizing the first ten non-zero eigenvalues.
@unpublished{antunes:hal-03676230,
TITLE = {{Optimization of the Steklov-Lam{\'e} eigenvalues with respect to the domain}},
AUTHOR = {Antunes, Pedro and Bogosel, Beniamin},
URL = {https://hal.archives-ouvertes.fr/hal-03676230},
NOTE = {working paper or preprint},
YEAR = {2022},
MONTH = May,
KEYWORDS = {shape optimization ; Steklov-Lam{\'e} eigenvalues ; fundamental solutions},
PDF = {https://hal.archives-ouvertes.fr/hal-03676230/file/SteklovLame.pdf},
HAL_ID = {hal-03676230},
HAL_VERSION = {v1},
}
B. Bogosel, D. Bucur,
On the polygonal Faber-Krahn inequality, 2022
(accepted in Journal de l’École polytechnique — Mathématiques) (
hal-03625471) (
arxiv:2203.16409)
Abstract
Bibtex
Details
It has been conjectured by Pólya and Szegö seventy years ago that the planar set which minimizes the first eigenvalue of the Dirichlet-Laplace operator among polygons with $n$ sides and fixed area is the regular polygon. Despite its apparent simplicity, this result has only been proved for triangles and quadrilaterals. In this paper we prove that for each $n \ge 5$ the proof of the conjecture can be reduced to a finite number of certified numerical computations. Moreover, the local minimality of the regular polygon can be reduced to a single numerical computation. For $n=5, 6,7, 8$ we perform this computation and certify the numerical approximation by finite elements, up to machine errors.
@unpublished{bogosel:hal-03625471,
TITLE = {{On the polygonal Faber-Krahn inequality}},
AUTHOR = {Bogosel, Beniamin and Bucur, Dorin},
URL = {https://hal.archives-ouvertes.fr/hal-03625471},
NOTE = {working paper or preprint},
YEAR = {2022},
MONTH = Mar,
PDF = {https://hal.archives-ouvertes.fr/hal-03625471/file/submitted.pdf},
HAL_ID = {hal-03625471},
HAL_VERSION = {v1},
}
B. Bogosel
Numerical shape optimization among convex sets, 2022
(accepted in Applied Mathematics and Optimization) (
hal-03607776) (
arxiv:2203.06981)
Abstract
Bibtex
This article proposes a new discrete framework for approximating solutions to
shape optimization problems under convexity constraints. The numerical method,
based on the support function or the gauge function, is guaranteed to generate discrete convex shapes and is easily implementable using standard optimization software. The framework can handle various objective functions ranging from geometric
quantities to functionals depending on partial differential equations. Width or diameter constraints are handled using the support function. Functionals depending
on a convex body and its polar body can be handled using a unified framework
@unpublished{bogosel:hal-03607776,
TITLE = {{Numerical shape optimization among convex sets}},
AUTHOR = {Bogosel, Beniamin},
URL = {https://hal.archives-ouvertes.fr/hal-03607776},
NOTE = {working paper or preprint},
YEAR = {2022},
MONTH = Mar,
KEYWORDS = {Shape optimization ; convex shapes ; numerical simulations ; support function ; gauge function MSC Classifications: 49Q10 ; 52A27},
PDF = {https://hal.archives-ouvertes.fr/hal-03607776/file/DiscreteConvex.pdf},
HAL_ID = {hal-03607776},
HAL_VERSION = {v1},
}
M. Godoy, G. Allaire, B. Bogosel
Topology optimization of supports with imperfect
bonding in additive manufacturing, 2021
(to appear in Structural and Multidisciplinary Optimization) (
hal-03538224)
Abstract
Bibtex
Supports are an important ingredient of the building process of structures by additive manufacturing technologies. They are used to reinforce overhanging regions of the
desired structure and/or to facilitate the mitigation of residual thermal stresses due to
the extreme heat flux produced by the source term (laser beam). Very often, supports
are, on purpose, weakly connected to the built structure for easing their removal. In
this work we consider an imperfect interface model for which the interaction between
supports and the built structure is not ideal, meaning that the displacement is discontinuous at the interface while the normal stress is continuous and proportional to the
jump of the displacement. The optimization process is based on the level set method,
body fitted meshes and the notion of shape derivative using the adjoint method. We
provide 2-d and 3-d numerical examples, as well as a comparison with the usual perfect
interface model. Completely different designs of supports are obtained with perfect or
imperfect interfaces.
@unpublished{allaire:hal-03538224,
TITLE = {{Topology optimization of supports with imperfect bonding in additive manufacturing}},
AUTHOR = {Allaire, Gr{\'e}goire and Bogosel, Beniamin and Godoy, Mat{\'i}as},
URL = {https://hal.archives-ouvertes.fr/hal-03538224},
NOTE = {working paper or preprint},
YEAR = {2022},
MONTH = Jan,
KEYWORDS = {Imperfect interface ; interfacial rigidity ; support optimization ; topology optimization ; level set method},
PDF = {https://hal.archives-ouvertes.fr/hal-03538224/file/ElasImag-Janvier.pdf},
HAL_ID = {hal-03538224},
HAL_VERSION = {v1},
}
M. Bihr, G. Allaire, X Betbeder-Lauque, B. Bogosel, F. Bordeu, J. Querois
Part and supports optimization in metal powder bed
additive manufacturing using simplified process
simulation, 2021
(to appear in Computer Methods in Applied Mechanics and Engineering) (
hal-03507990)
Abstract
Bibtex
This paper is concerned with shape and topology optimization of parts and their supports, taking into account constraints coming from the metal powder bed additive manufacturing process. Despite the high complexity of this process, it is represented by the simple inherent strain model, which has the advantage of being computationally cheap. Three optimization criteria, evaluated with this model, are proposed to minimize defects caused by additive manufacturing: vertical displacements, residual stresses and deflection of the part after baseplate separation. Combining these criteria with a constraint on the compliance for the final use of the part leads to optimization problems which deliver optimized manufacturable shapes with only a slight loss on the final use performance. The numerical results are assessed by manufacturing some optimized and reference geometries. These experimental results are also used to calibrate the inherent strain model by an inverse analysis. The same type of optimization is applied to supports in the case of a fixed non-optimizable part. For our 3-d numerical tests we rely on the level set method, the notion of shape derivatives and an augmented Lagrangian algorithm for optimization.
@unpublished{bihr:hal-03507990,
TITLE = {{Part and supports optimization in metal powder bed additive manufacturing using simplified process simulation}},
AUTHOR = {Bihr, Martin and Allaire, Gr{\'e}goire and Betbeder-Lauque, Xavier and Bogosel, Beniamin and Bordeu, Felipe and Querois, Julie},
URL = {https://hal.archives-ouvertes.fr/hal-03507990},
NOTE = {working paper or preprint},
YEAR = {2022},
MONTH = Jan,
PDF = {https://hal.archives-ouvertes.fr/hal-03507990/file/manuscript_topology_inherent.pdf},
HAL_ID = {hal-03507990},
HAL_VERSION = {v1},
}
B. Bogosel, E. Oudet,
Longest minimal length partitions, 2021
(to appear in Interfaces and Free Boundaries) (
hal-03132237) (
arxiv:2102.02891)
Abstract
Numerics
Bibtex
This article provides numerical evidence that under volume constraint the ball is the set which maximizes the perimeter of the least-perimeter partition into cells with prescribed areas. We introduce a numerical maximization algorithm which performs multiple optimizations steps at each iteration to approximate minimal partitions. Using these partitions we compute perturbations of the domain which increase the minimal perimeter. The initialization of the optimal partitioning algorithm uses capacity-constrained Voronoi diagrams. A new algorithm is proposed to identify such diagrams, by computing the gradients of areas and perimeters for the Voronoi cells with respect to the Voronoi points.
 |
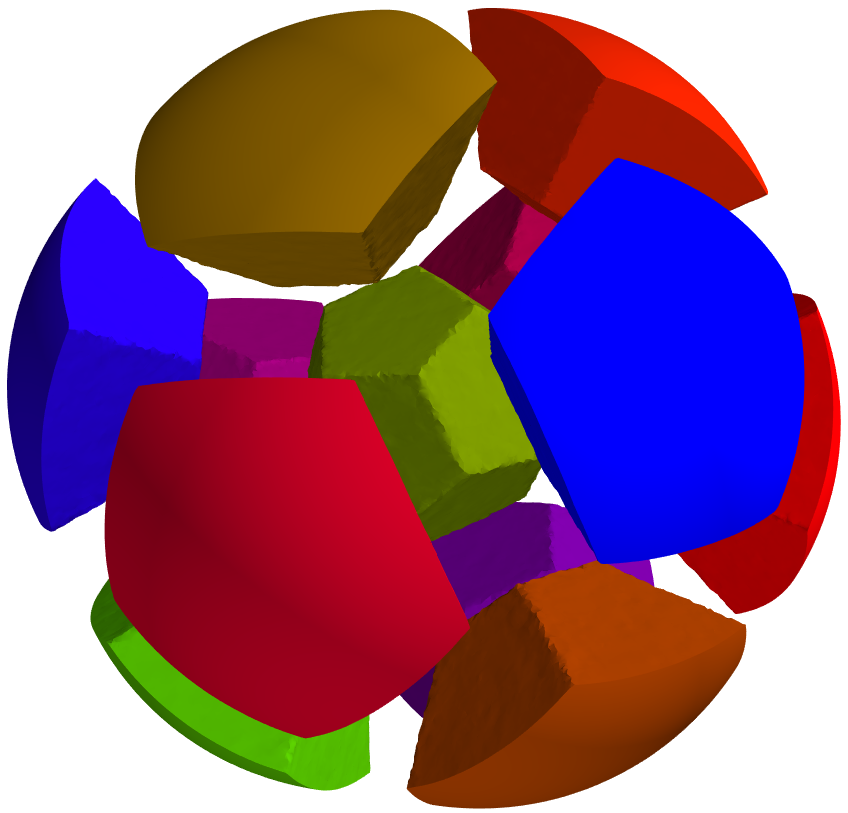Click on one of the pictures for details concerning numerical results |
@misc{2102.02891,
Author = {Beniamin Bogosel and Edouard Oudet},
Title = {Longest minimal length partitions},
Year = {2021},
Eprint = {arXiv:2102.02891},
}
M. Godoy, G. Allaire, B. Bogosel,
Shape optimization of an imperfect interface: steady-state heat diffusion, 2020
(to appear in Journal of Optimization Theory and Applications) (
hal-03102760)
Abstract
Numerics
Bibtex
In the context of a diffusion equation, this work is devoted to a two-phase optimal design problem where the interface, separating the phases, is imperfect, meaning that the solution is discontinuous while the normal flux is continuous and proportional to the jump of the solution. The shape derivative of an objective function with respect to the interface position is computed by the adjoint method. Numerical experiments are performed with the level set method and an exact remeshing algorithm so that the interface is captured by the mesh at each optimization iteration. Comparisons with a perfect interface are discussed in the setting of optimal design or inverse problems.
 |
Click on one of the pictures for details concerning numerical results |
@unpublished{hal-03102760,
TITLE = {{Shape optimization of an imperfect interface: steady-state heat diffusion}},
AUTHOR = {Allaire, Gr{\'e}goire and Bogosel, Beniamin and Godoy, Matias},
URL = {https://hal.archives-ouvertes.fr/hal-03102760},
NOTE = {working paper or preprint},
YEAR = {2021},
MONTH = Jan,
KEYWORDS = {imperfect interfaces ; shape optimization ; level set method},
PDF = {https://hal.archives-ouvertes.fr/hal-03102760/file/Interface_Scalaire-Greyscale_final.pdf},
HAL_ID = {hal-03102760},
HAL_VERSION = {v1},
}
B. Bogosel, T. Giletti, A. Tellini,
Propagation for KPP bulk-surface systems in a general
cylindrical domain, 2020
(to appear in Nonlinear Analysis) (
hal-02880034) (
arxiv:2006.14224 )
Abstract
Numerics
Bibtex
In this paper, we investigate propagation phenomena for KPP bulk-surface systems in
a cylindrical domain with general section and heterogeneous coefficients. As for the scalar
KPP equation, we show that the asymptotic spreading speed of solutions can be computed
in terms of the principal eigenvalues of a family of self-adjoint elliptic operators.
Using this characterization, we analyze the dependence of the spreading speed on various
parameters, including diffusion rates and the size and shape of the section of the domain. In
particular, we provide new theoretical results on several asymptotic regimes like small and
high diffusion rates and sections with small and large sizes. These results generalize earlier
ones which were available in the radial homogeneous case.
Finally, we numerically investigate the issue of shape optimization of the spreading speed.
By computing its shape derivative, we observe, in the case of homogeneous coefficients, that
a disk either maximizes or minimizes the speed, depending on the parameters of the problem,
both with or without constraints. We also show the results of numerical shape optimization
with non homogeneous coefficients, when the disk is no longer an optimizer.
|
Click on one of the pictures for details concerning numerical results |
@misc{2006.14224,
Author = {Beniamin Bogosel and Thomas Giletti and Andrea Tellini},
Title = {Propagation for KPP bulk-surface systems in a general cylindrical domain},
Year = {2020},
Eprint = {arXiv:2006.14224},
}
A. Al Sayed, B. Bogosel, A. Henrot, F. Nacry,
Maximization of the Steklov Eigenvalues with a Diameter Constraint
SIAM Journal on Mathematical Analysis, 53(1), 2021
Abstract
Numerics
Bibtex
In this paper, we address the problem of maximizing the Steklov eigenvalues with
a diameter constraint. We provide an estimate of the Steklov eigenvalues for a convex domain
in terms of its diameter and volume and we show the existence of an optimal convex domain.
We establish that balls are never maximizers, even for the first non-trivial eigenvalue that
contrasts with the case of volume or perimeter constraints. Under an additional regularity
assumption, we are able to prove that the Steklov eigenvalue is multiple for the optimal
domain. We illustrate our theoretical results by giving some optimal domains in the plane
thanks to a numerical algorithm.
 |
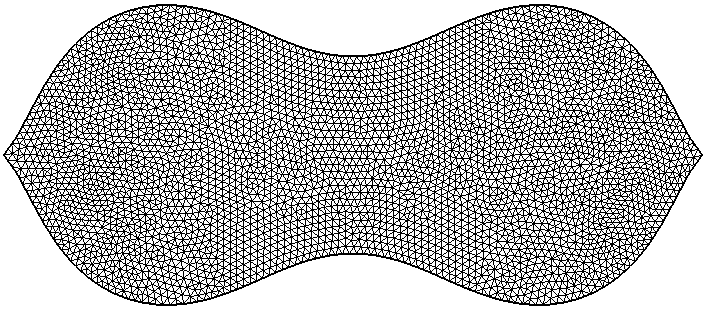Click on one of the pictures for details concerning numerical results |
@article{ABBH21,
doi = {10.1137/20m1335042},
url = {https://doi.org/10.1137/20m1335042},
year = {2021},
month = jan,
publisher = {Society for Industrial {\&} Applied Mathematics ({SIAM})},
volume = {53},
number = {1},
pages = {710--729},
author = {Abdelkader Al Sayed and Beniamin Bogosel and Antoine Henrot and Florent Nacry},
title = {Maximization of the Steklov Eigenvalues With a Diameter Constraint},
journal = {{SIAM} Journal on Mathematical Analysis}
}
G. Allaire, M. Bihr, B. Bogosel,
Support optimization in additive manufacturing for geometric and thermo-mechanical constraints Structural and Multidisciplinary Optimization, 61(6), 2020
Abstract
Numerics
Bibtex
Supports are often required to safely complete the building of complicated structures
by additive manufacturing technologies. In particular, supports are used as scaffoldings to
reinforce overhanging regions of the structure and/or are necessary to mitigate the ther-
mal deformations and residual stresses created by the intense heat flux produced by the
source term (typically a laser beam). However, including supports increase the fabrica-
tion cost and their removal is not an easy matter. Therefore, it is crucial to minimize their
volume while maintaining their efficiency. Based on earlier works, we propose here some
new optimization criteria. First, simple geometric criteria are considered like the projected
area and the volume of supports required for overhangs: they are minimized by varying
the structure orientation with respect to the baseplate. In addition, an accessibility crite-
rion is suggested for the removal of supports, which can be used to forbid some parts of
the structure to be supported. Second, shape and topology optimization of supports for
compliance minimization is performed. The novelty comes from the applied surface loads
which are coming either from pseudo gravity loads on overhanging parts or from equiva-
lent thermal loads arising from the layer by layer building process. Here, only the supports
are optimized, with a given non-optimizable structure, but of course many generalizations
are possible, including optimizing both the structure and its supports. Our optimization
algorithm relies on the level set method and shape derivatives computed by the Hadamard
method. Numerical examples are given in 2-d and 3-d.
 |
Click on one of the pictures for details concerning numerical results |
@article{AlBiBo2020,
doi = {10.1007/s00158-020-02551-1},
url = {https://doi.org/10.1007/s00158-020-02551-1},
year = {2020},
month = apr,
publisher = {Springer Science and Business Media {LLC}},
volume = {61},
number = {6},
pages = {2377--2399},
author = {Gr{\'{e}}goire Allaire and Martin Bihr and Beniamin Bogosel},
title = {Support optimization in additive manufacturing for geometric and thermo-mechanical constraints},
journal = {Structural and Multidisciplinary Optimization}
}
P. Antunes, B. Bogosel,
Parametric Shape Optimization using the Support Function
to appear in Computational Optimization and Applications, (
arxiv:1809.00254)
Abstract
Numerics
Bibtex
The optimization of functionals depending on shapes which have convexity, diameter or constant width constraints is difficult from a numerical point of view. We show how to use the support function in order to approximate solutions to such problems by finite dimensional optimization problems under various constraints. After constructing the numerical framework, we present some applications from the field of convex geometry. We consider the optimization of various functionals depending on the volume, perimeter and Dirichlet Laplace eigenvalues under the constraints presented earlier. In particular we confirm numerically Meissner's conjecture, regarding three dimensional bodies of constant width with minimal volume, by directly solving an optimization problem.
 |
Click on one of the pictures for details concerning numerical results |
@misc{1809.00254,
Author = {Pedro R. S. Antunes and Beniamin Bogosel},
Title = {Parametric Shape Optimization using the Support Function},
Year = {2018},
Eprint = {arXiv:1809.00254},
}
B. Bogosel, V. Perrollaz, K. Raschel, A. Trotignon,
3D positive lattice walks and spherical triangles
Journal of Combinatorial Theory, Series A, 172, 2020
Abstract
Numerics
Bibtex
In this paper we explore the asymptotic enumeration of three-dimensional
excursions confined to the positive octant. As shown in [29], both the exponential
growth and the critical exponent admit universal formulas, respectively in terms of the
inventory of the step set and of the principal Dirichlet eigenvalue of a certain spherical
triangle, itself being characterized by the steps of the model. We focus on the critical
exponent, and our main objective is to relate combinatorial properties of the step set
(structure of the so-called group of the walk, existence of a Hadamard factorization,
existence of differential equations satisfied by the generating functions) to geometric
or analytic properties of the associated spherical triangle (remarkable angles, tiling
properties, existence of an exceptional closed-form formula for the principal eigenvalue).
As in general the eigenvalues of the Dirichlet problem on a spherical triangle are not
known in closed form, we also develop a finite-elements method to compute approximate
values, typically with ten digits of precision.
 |
Click on one of the pictures for details concerning numerical results |
@article{BPRT2020,
doi = {10.1016/j.jcta.2019.105189},
url = {https://doi.org/10.1016/j.jcta.2019.105189},
year = {2020},
month = may,
publisher = {Elsevier {BV}},
volume = {172},
pages = {105189},
author = {B. Bogosel and V. Perrollaz and K. Raschel and A. Trotignon},
title = {3D positive lattice walks and spherical triangles},
journal = {Journal of Combinatorial Theory, Series A}
}
G. Allaire, B. Bogosel,
Optimizing supports for additive manufacturing
Structural and Multidisciplinary Optimization, 58(6), 2018
Abstract
Numerics
Bibtex
In additive manufacturing process support structures are often required to ensure the
quality of the final built part. In this article we present mathematical models and their numerical
implementations in an optimization loop, which allow us to design optimal support
structures. Our models are derived with the requirement that they should be as simple as
possible, computationally cheap and yet based on a realistic physical modeling. Supports
are optimized with respect to two different physical properties. First, they must support
overhanging regions of the structure for improving the stiffness of the supported structure
during the building process. Second, supports can help in channeling the heat flux produced
by the source term (typically a laser beam) and thus improving the cooling down
of the structure during the fabrication process. Our optimization algorithm is based on the
level set method and on the computation of shape derivatives by the Hadamard method. In
a first approach, only the shape and topology of the supports are optimized, for a given and
fixed structure. In second and more elaborated strategy, both the supports and the structure
are optimized, which amounts to a specific multiphase optimization problem. Numerical
examples are given in 2-d and 3-d.
 |
Click on one of the pictures for details concerning numerical results |
@article{AllaireBogosel2018,
doi = {10.1007/s00158-018-2125-x},
url = {https://doi.org/10.1007/s00158-018-2125-x},
year = {2018},
month = oct,
publisher = {Springer Science and Business Media {LLC}},
volume = {58},
number = {6},
pages = {2493--2515},
author = {Gr{\'{e}}goire Allaire and Beniamin Bogosel},
title = {Optimizing supports for additive manufacturing},
journal = {Structural and Multidisciplinary Optimization}
}
B. Bogosel, A. Henrot, I. Lucardesi,
Minimization of the eigenvalues of the Dirichlet-Laplacian with a diameter constraint SIAM Journal on Mathematical Analysis, 50(5), 2018
Abstract
Numerics
Bibtex
In this paper we look for the domains minimizing the $h$-th eigenvalue of the Dirichlet-Laplacian $\lambda_h$
with a constraint on the diameter. Existence of an optimal domain is easily obtained, and is attained at a constant width body. In the case of a simple eigenvalue, we provide non standard (i.e., non local) optimality conditions. Then we address the question whether or not the disk is an optimal domain in the plane, and we give the precise list of the 17 eigenvalues for which the disk is a local minimum. We conclude by some numerical simulations showing the 20 first optimal domains in the plane.
 |
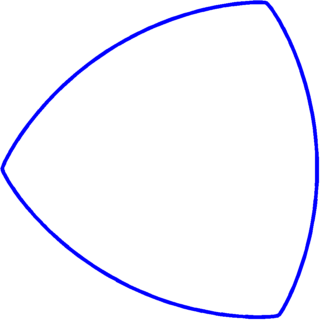Click on one of the pictures for details concerning numerical results |
@article{BoHeLu18,
doi = {10.1137/17m1162147},
url = {https://doi.org/10.1137/17m1162147},
year = {2018},
month = jan,
publisher = {Society for Industrial {\&} Applied Mathematics ({SIAM})},
volume = {50},
number = {5},
pages = {5337--5361},
author = {B. Bogosel and A. Henrot and I. Lucardesi},
title = {Minimization of the Eigenvalues of the Dirichlet-Laplacian with a Diameter Constraint},
journal = {{SIAM} Journal on Mathematical Analysis}
}
B. Bogosel, D. Bucur, I. Fragala,
Phase field approach to optimal packing problems and related Cheeger clusters Applied Mathematics and Optimization, 81(1), 2018
Abstract
Numerics
Bibtex
In a fixed domain of $\Bbb{R} ^N$ we study the asymptotic behaviour of optimal clusters associated to $\alpha$-Cheeger constants and natural energies like the sum or maximum: we prove that, as the parameter $\alpha$ converges to the ``critical" value $\Big (\frac{N-1}{N}\Big ) _+$, optimal Cheeger clusters converge to solutions of different packing problems for balls, depending on the energy under consideration. As well, we propose an efficient phase field approach based on a multiphase Gamma convergence result of Modica-Mortola type, in order to compute $\alpha$-Cheeger constants, optimal clusters and, as a consequence of the asymptotic result, optimal packings. Numerical experiments are carried over in two and three space dimensions.
 |
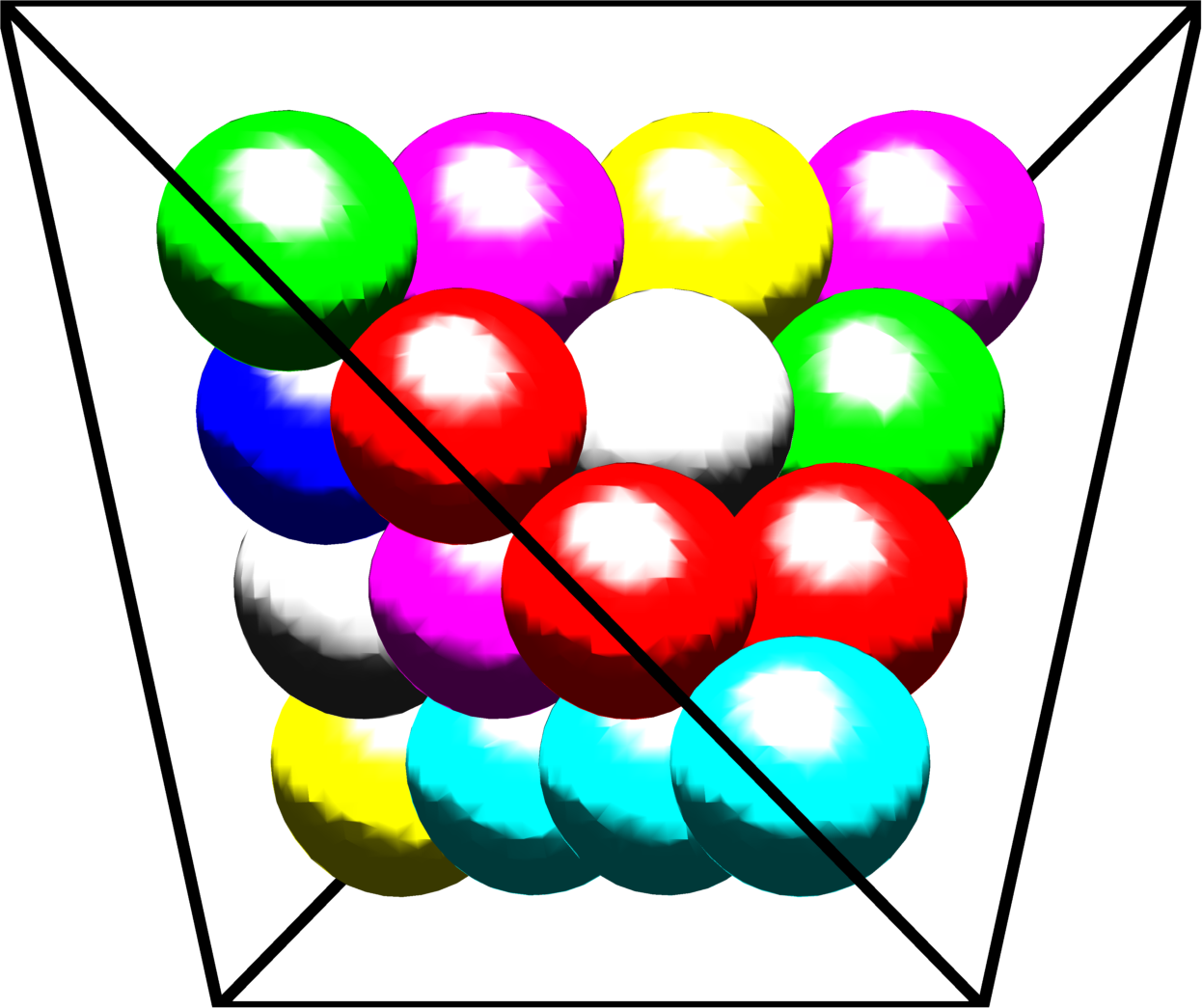Click on one of the pictures for details concerning numerical results |
@article{BoBuFr18,
doi = {10.1007/s00245-018-9476-y},
url = {https://doi.org/10.1007/s00245-018-9476-y},
year = {2018},
month = feb,
publisher = {Springer Science and Business Media {LLC}},
volume = {81},
number = {1},
pages = {63--87},
author = {Beniamin Bogosel and Dorin Bucur and Ilaria Fragal{\`{a}}},
title = {Phase Field Approach to Optimal Packing Problems and Related Cheeger Clusters},
journal = {Applied Mathematics {\&} Optimization}
}
B. Bogosel,
Efficient algorithm for optimizing spectral partitions
Applied Mathematics and Computation, 333, 2018
Abstract
Numerics
Bibtex
We present an amelioration of current known algorithms for optimal spectral partitioning problems. The idea is to use the advantage of a representation using density functions
while decreasing the computational time. This is done by restricting the computation to
neighbourhoods of regions where the associated densities are above a certain threshold.
The algorithm extends and improves known methods in the plane and on surfaces in dimension 3. It also makes possible to make some of the first computations of volumic 3D
spectral partitions on sufficiently large discretizations.
 |
 |
Click on one of the pictures for details concerning numerical results |
@article{BogoselEigPart2018,
doi = {10.1016/j.amc.2018.03.087},
url = {https://doi.org/10.1016/j.amc.2018.03.087},
year = {2018},
month = sep,
publisher = {Elsevier {BV}},
volume = {333},
pages = {61--75},
author = {Beniamin Bogosel},
title = {Efficient algorithm for optimizing spectral partitions},
journal = {Applied Mathematics and Computation}
}
B. Bogosel, V. Bonnaillie-Noël,
Minimal Partitions for p-norms of Eigenvalues
Interfaces and Free Boundaries, 20(1), 2018
Abstract
Numerics
Bibtex
In this article we are interested in studying partitions of the square, the disk and the equilateral triangle which minimize a p-norm of eigenvalues of the Dirichlet-Laplace operator. The extremal case of the infinity norm, where we minimize the largest fundamental eigenvalue of each cell, is one of our main interests. We propose three numerical algorithms which approximate the optimal configurations and we obtain tight upper bounds for the energy, which are better than the ones given by theoretical results. A thorough comparison of the results obtained by the three methods is given. We also investigate the behavior of the minimal partitions with respect to p. This allows us to see when partitions minimizing the 1-norm and the infinity-norm are different.
 |
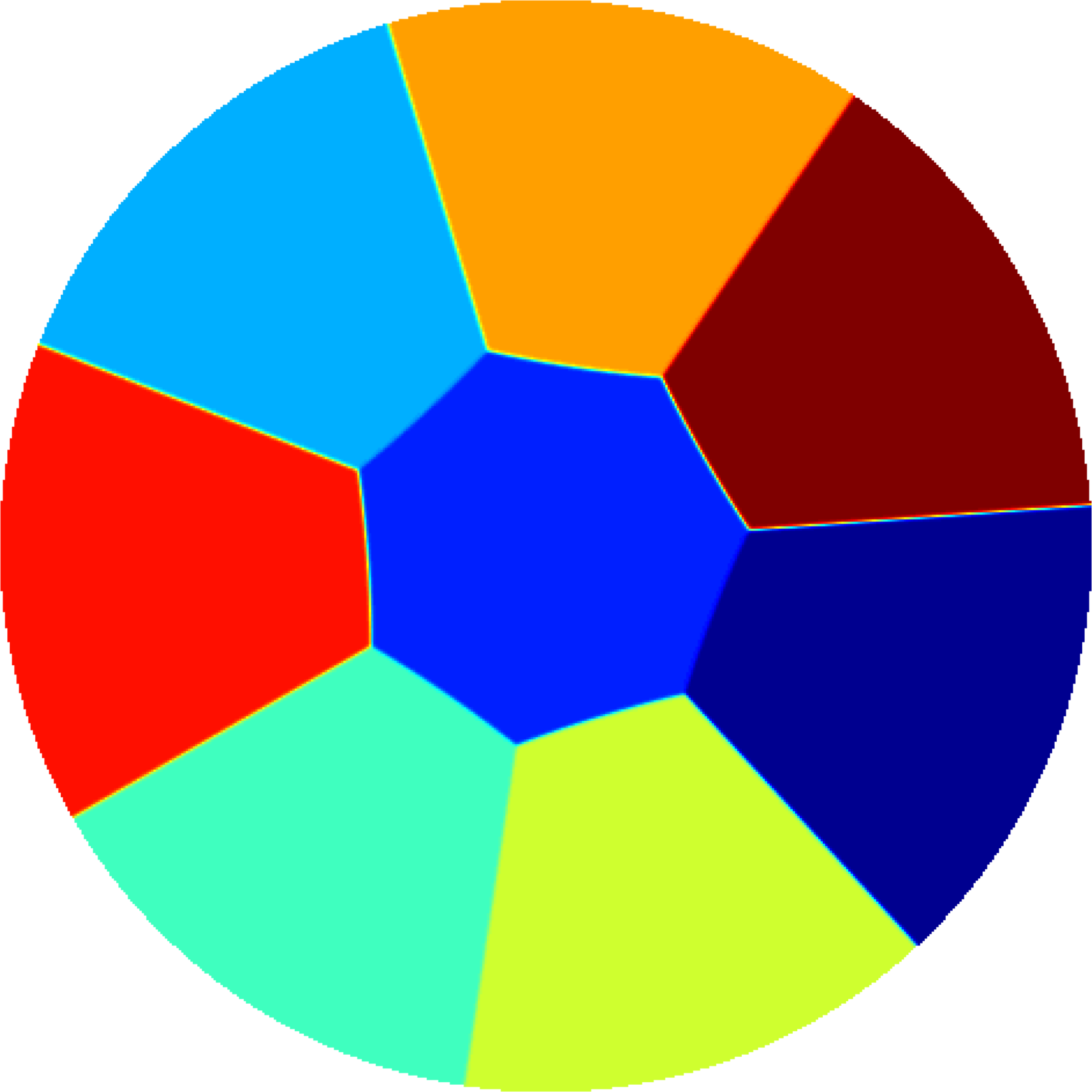For details click on one of the pictures. |
@article{BoBN2018,
doi = {10.4171/ifb/399},
url = {https://doi.org/10.4171/ifb/399},
year = {2018},
month = may,
publisher = {European Mathematical Society Publishing House},
volume = {20},
number = {1},
pages = {129--163},
author = {Beniamin Bogosel and Virginie Bonnaillie-Noël},
title = {Minimal partitions for {\textdollar}p{\textdollar}-norms of eigenvalues},
journal = {Interfaces and Free Boundaries}
}
B. Bogosel,
Regularity result for a shape optimization problem under
perimeter constraint
Communications in Analysis and Geometry, 27(7), 2019
Abstract
Bibtex
We study the problem of optimizing the eigenvalues of the Dirichlet Laplace operator
under perimeter constraint. We prove that optimal sets are smooth by writing a general
optimality condition in the case the optimal eigenvalue is multiple. As a consequence we find
that the optimal $k$-th eigenvalue is strictly smaller than the optimal $k+1$-th eigenvalue. We
also provide an elliptic regularity result for sets with positive and bounded weak curvature.
 |
 |
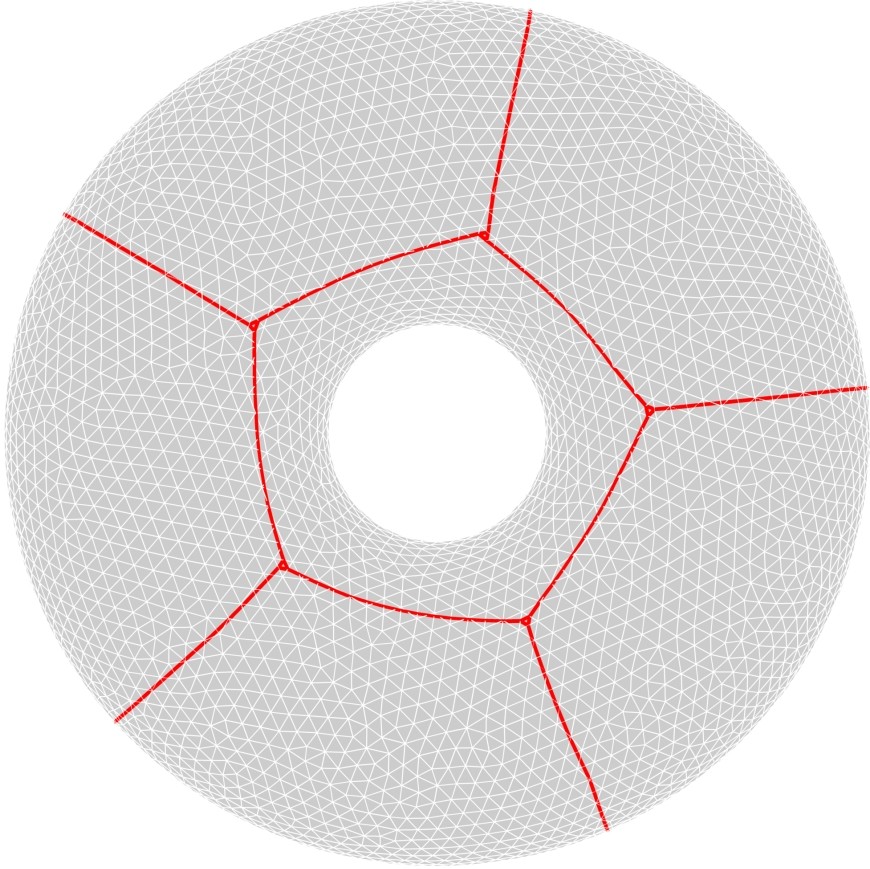For details click on one of the pictures. |
@article{BogoselRegularity2019,
doi = {10.4310/cag.2019.v27.n7.a3},
url = {https://doi.org/10.4310/cag.2019.v27.n7.a3},
year = {2019},
publisher = {International Press of Boston},
volume = {27},
number = {7},
pages = {1523--1547},
author = {Beniamin Bogosel},
title = {Regularity result for a shape optimization problem under perimeter constraint},
journal = {Communications in Analysis and Geometry}
}
B. Bogosel, E. Oudet,
Partitions of Mimimal Length on Manifolds,
Experimental Mathematics, 26(4), 2016
Abstract
Numerics
Bibtex
We study partitions on three dimensional manifolds which minimize the total geodesic perimeter.
We propose a relaxed framework based on a $\Gamma$-convergence result and we show some numerical results.
We compare our results to those already present in the literature in the case of the sphere.
For general surfaces we provide an optimization algorithm on meshes which can give a good approximation of the optimal cost,
starting from the results obtained using the relaxed formulation.
|
|
For details click on one of the pictures. |
@article{BogoselOudetManifolds2016,
doi = {10.1080/10586458.2016.1223570},
url = {https://doi.org/10.1080/10586458.2016.1223570},
year = {2016},
month = oct,
publisher = {Informa {UK} Limited},
volume = {26},
number = {4},
pages = {496--508},
author = {Beniamin Bogosel and {\'{E}}douard Oudet},
title = {Partitions of Minimal Length on Manifolds},
journal = {Experimental Mathematics}
}
B. Bogosel, D. Bucur, A. Giacomini,
Optimal Shapes Maximizing the Steklov Eigenvalues,
SIAM Journal on Mathematical Analysis, 49(2), 2017 (
Journal link)
Abstract
Numerics
Bibtex
In this paper we consider the problem of maximizing the $k$-th Steklov eigenvalue of
the Laplacian (or a more general spectral functional), among all sets of $\Bbb{R}^d$ of prescribed volume.
We prove existence of an optimal set and get some qualitative properties of the solutions in a relaxed setting.
In particular, in $\Bbb{R}^2$, we prove that the optimal set consists in the union of at
most $k$ disjoint Jordan domains with finite perimeter. A key point of our analysis is played by
an isodiametric control of the Stelkov spectrum. We also perform some numerical experiments
and exhibit the optimal shapes maximizing the $k$-th eigenvalues under area constraint in $\Bbb{R}^2$, for
$k = 1,...,10$.
 |
For details click on one of the pictures. |
@article{BoBuGi2017,
doi = {10.1137/16m1075260},
url = {https://doi.org/10.1137/16m1075260},
year = {2017},
month = jan,
publisher = {Society for Industrial {\&} Applied Mathematics ({SIAM})},
volume = {49},
number = {2},
pages = {1645--1680},
author = {B. Bogosel and D. Bucur and A. Giacomini},
title = {Optimal Shapes Maximizing the Steklov Eigenvalues},
journal = {{SIAM} Journal on Mathematical Analysis}
}
B. Bogosel,
The method of fundamental solutions
applied to boundary eigenvalue problems,
Journal of Computational and Applied Mathematics, 306, 2016
(
Journal link)
Abstract
Numerics
Bibtex
We develop methods based on fundamental solutions to compute the Steklov,
Wentzell and Laplace-Beltrami eigenvalues. In the class of smooth simply connected two dimensional domains,
the numerical method is accurate and fast. A theoretical error bound is given along with comparisons with
mesh-based methods. We illustrate the use of this method in the study of a wide class of shape optimization
problems in two dimensions. We extend the method to the computation of the Laplace-Beltrami eigenvalues
on surfaces and we investigate some spectral optimal partitioning problems.
|
 |
 |
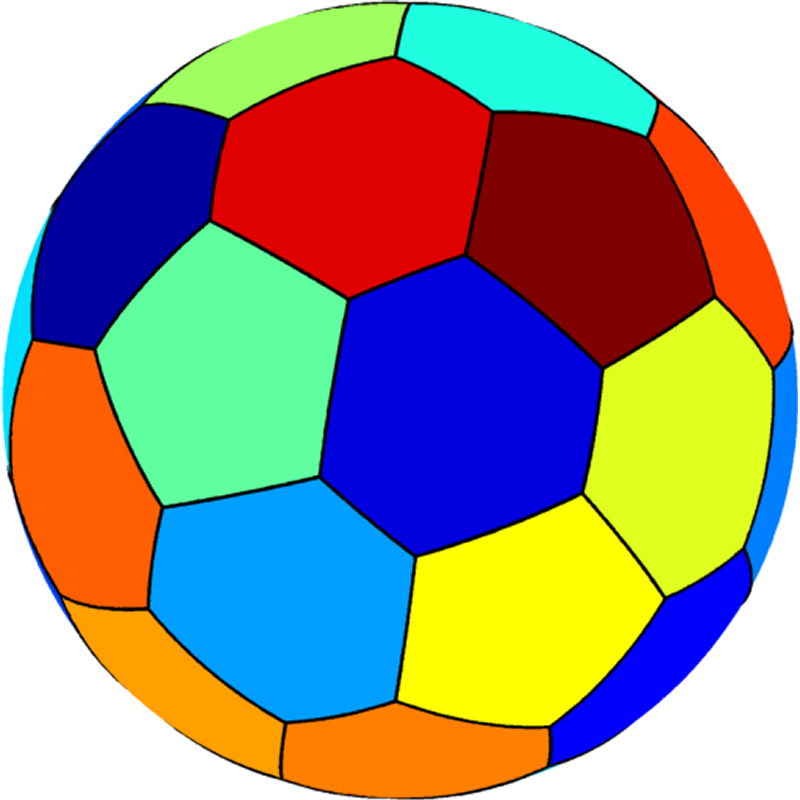For details click on one of the pictures. |
@article{Bogosel2016,
doi = {10.1016/j.cam.2016.04.008},
url = {https://doi.org/10.1016/j.cam.2016.04.008},
year = {2016},
month = nov,
publisher = {Elsevier {BV}},
volume = {306},
pages = {265--285},
author = {Beniamin Bogosel},
title = {The method of fundamental solutions applied to boundary eigenvalue problems},
journal = {Journal of Computational and Applied Mathematics}
}
B. Bogosel,
The Steklov spectrum on moving domains, 2015,
Applied Mathematics and Optimization, 75(1), 2015 (
Journal link)
Abstract
Bibtex
We study the continuity of the Steklov spectrum on variable
domains with respect to the Hausdorff convergence. A key point of the article
is understanding the behaviour of the traces of Sobolev functions on moving
boundaries of sets satisfying an uniform geometric condition.
As a consequence, we are able to prove existence results for shape optimization
problems regarding the Steklov spectrum in the family of sets satisfying
a $\varepsilon$-cone condition and in the family of convex sets.
@article{Bogosel2015,
doi = {10.1007/s00245-015-9321-5},
url = {https://doi.org/10.1007/s00245-015-9321-5},
year = {2015},
month = oct,
publisher = {Springer Science and Business Media {LLC}},
volume = {75},
number = {1},
pages = {1--25},
author = {Beniamin Bogosel},
title = {The Steklov Spectrum on Moving Domains},
journal = {Applied Mathematics {\&} Optimization}
}
B. Bogosel, E. Oudet,
Qualitative and Numerical Analysis
of a Spectral Problem with Perimeter Constraint, 2014
SIAM Journal on Control and Optimization, 54(1), 2016 (
Journal link)
Abstract
Numerics
Bibtex
We consider the problem of optimizing the
$k^{\text{th}}$ eigenvalue of Dirichlet Laplace operator under perimeter
constraint. We provide a new method based on a $\Gamma$-convergence result for
approximating the corresponding optimal shapes. We also give new optimality
conditions in the case of multiple eigenvalues. We deduce from previous
conditions the fact that optimal shapes never contain flat parts in their
boundaries.
 |
 |
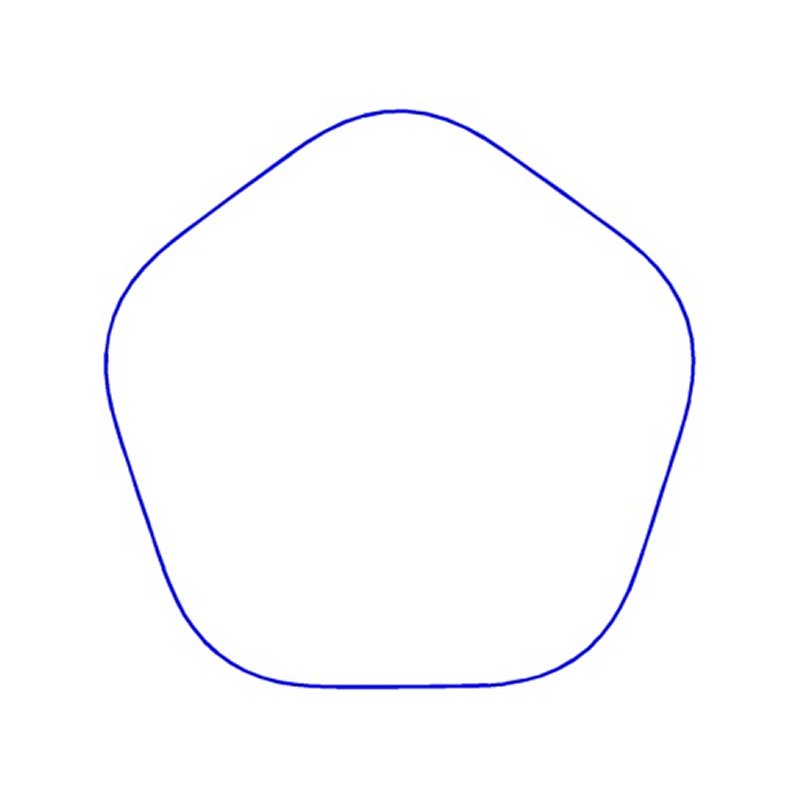For details click on one of the pictures. |
@article{BogoselOudet2016,
doi = {10.1137/140999530},
url = {https://doi.org/10.1137/140999530},
year = {2016},
month = jan,
publisher = {Society for Industrial {\&} Applied Mathematics ({SIAM})},
volume = {54},
number = {1},
pages = {317--340},
author = {Beniamin Bogosel and {\'{E}}douard Oudet},
title = {Qualitative and Numerical Analysis of a Spectral Problem with Perimeter Constraint},
journal = {{SIAM} Journal on Control and Optimization}
}
B. Bogosel, B. Velichkov,
A
multiphase shape optimization problem for eigenvalues: qualitative study
and numerical results SIAM Journal on Numerical Analysis, 54(1), 2016 (
Journal link)
Abstract
Numerics
Bibtex
We consider the multiphase shape optimization problem
$$\min\left\{\sum_{i=1}^h\lambda_1(\Omega_i)+\alpha|\Omega_i|:\ \Omega_i\
\hbox{open},\ \Omega_i\subset D,\ \Omega_i\cap\Omega_j=\emptyset\right\},$$
where $\alpha>0$ is a given constant and $D\subset\Bbb{R}^2$ is a bounded open
set with Lipschitz boundary. We give some new results concerning the qualitative
properties of the optimal sets and the regularity of the corresponding
eigenfunctions. We also provide numerical results for the optimal partitions.
 |
For details click on the picture. |
@article{BogoselVelichkov2016,
doi = {10.1137/140976406},
url = {https://doi.org/10.1137/140976406},
year = {2016},
month = jan,
publisher = {Society for Industrial {\&} Applied Mathematics ({SIAM})},
volume = {54},
number = {1},
pages = {210--241},
author = {Beniamin Bogosel and Bozhidar Velichkov},
title = {A Multiphase Shape Optimization Problem for Eigenvalues: Qualitative Study and Numerical Results},
journal = {{SIAM} Journal on Numerical Analysis}
}
