Beniamin BOGOSEL

Below you can find a list containing some numerical computations I performed. You can access a detailed version of each item by clicking on the associated picture.

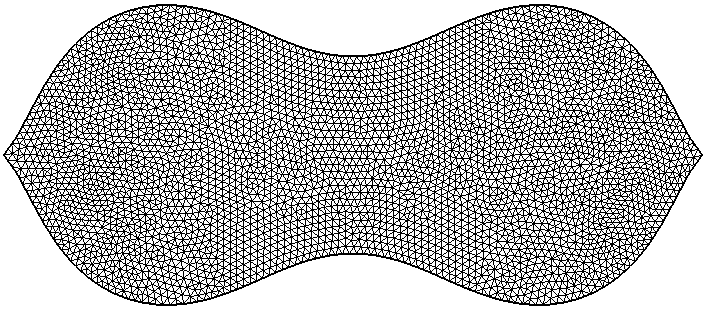
	Maximizing the Steklov eigenvalues with a diameter constraint
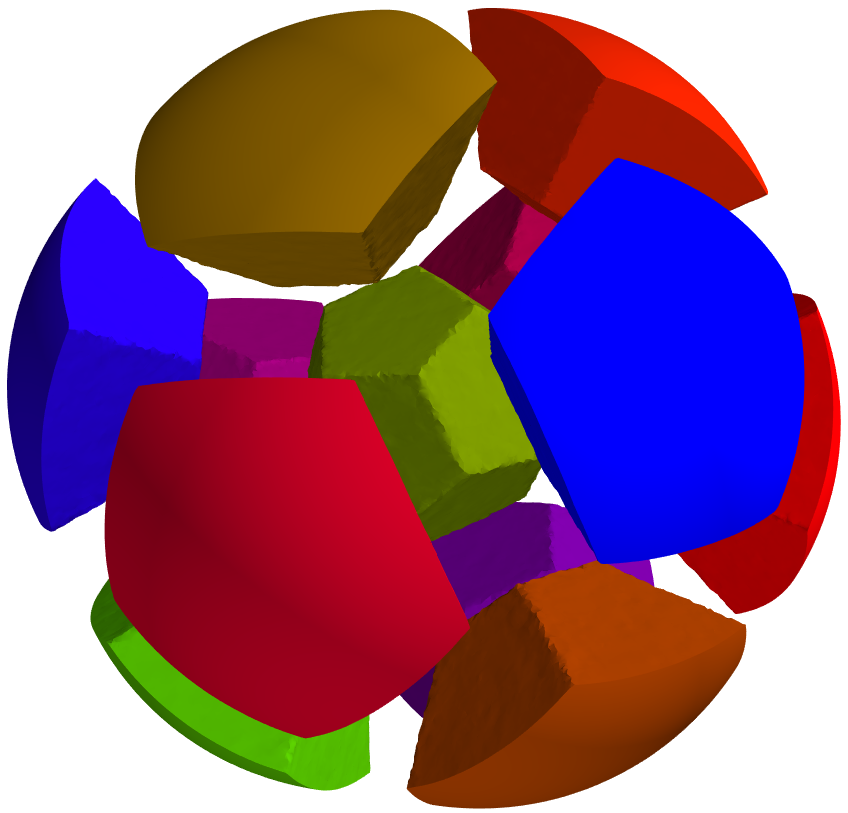	Maximizing the minimal relative perimeter of a partition
	Optimizing supports in additive manufacturing.
	Optimization of the supports in additive manufacturing: various models, numerical computations
	Optimization of various functionals under constant width/diameter and convexity constraints
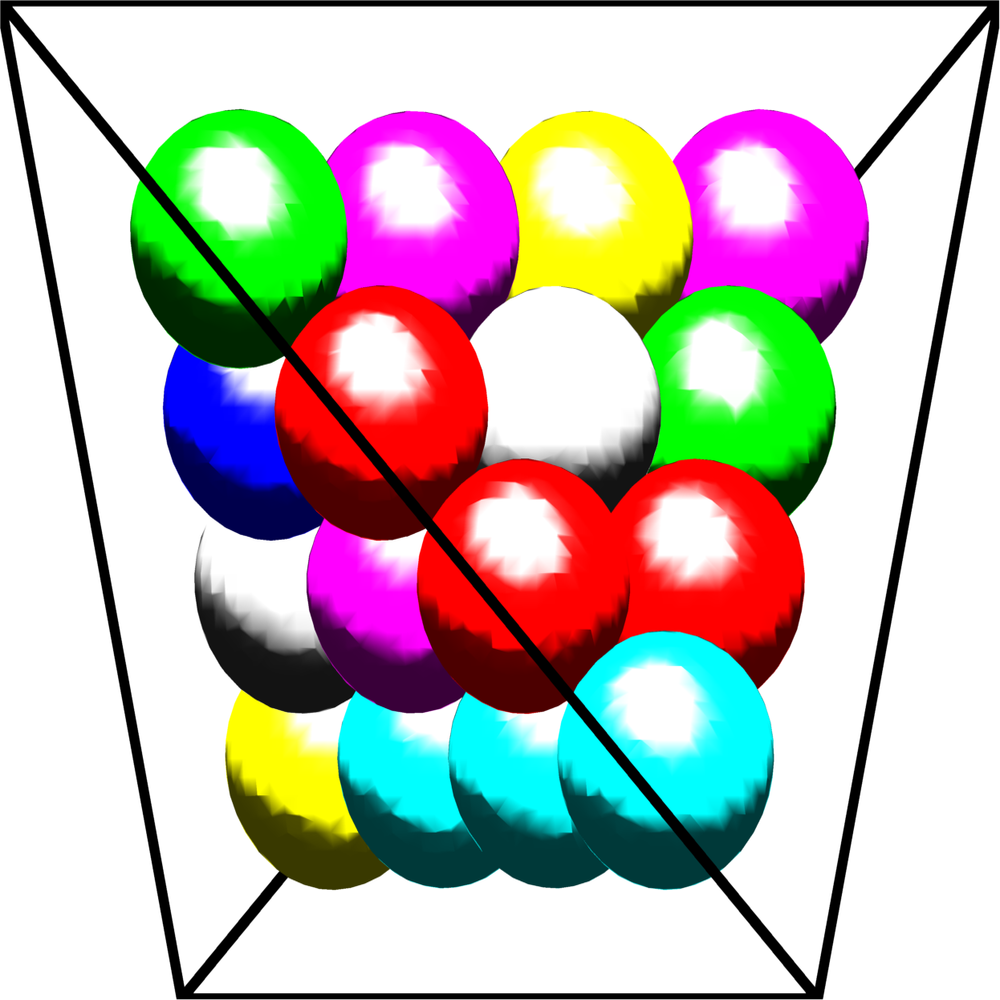	Computation of Cheeger sets and Circle/Sphere packings via a $\Gamma$-convergence relaxation
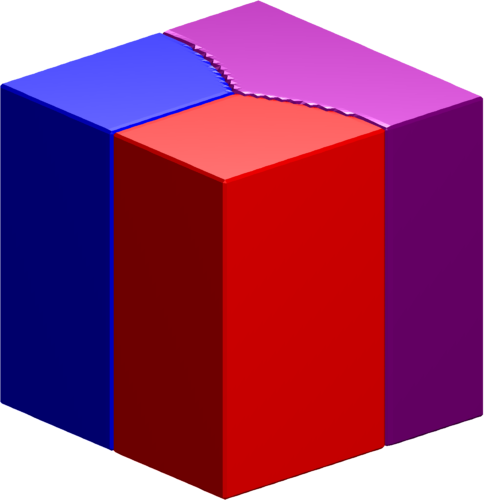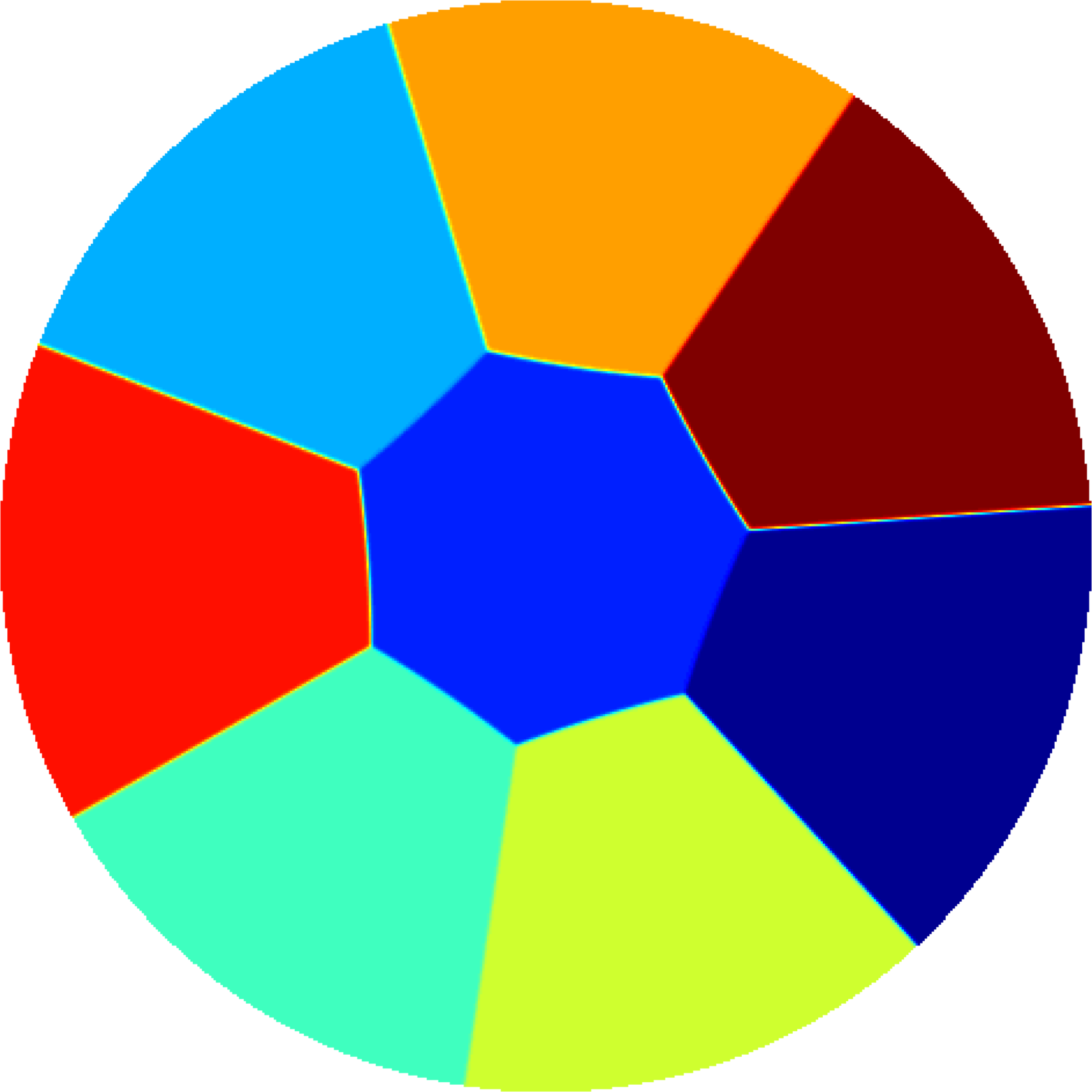
	Optimal partitions for eigenvalues in 3D
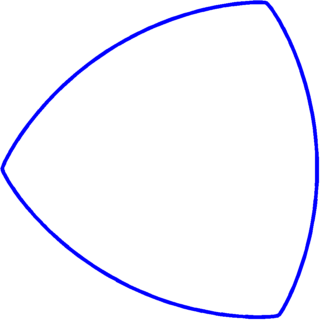	Eigenvalue optimization in the class of shapes of constant width
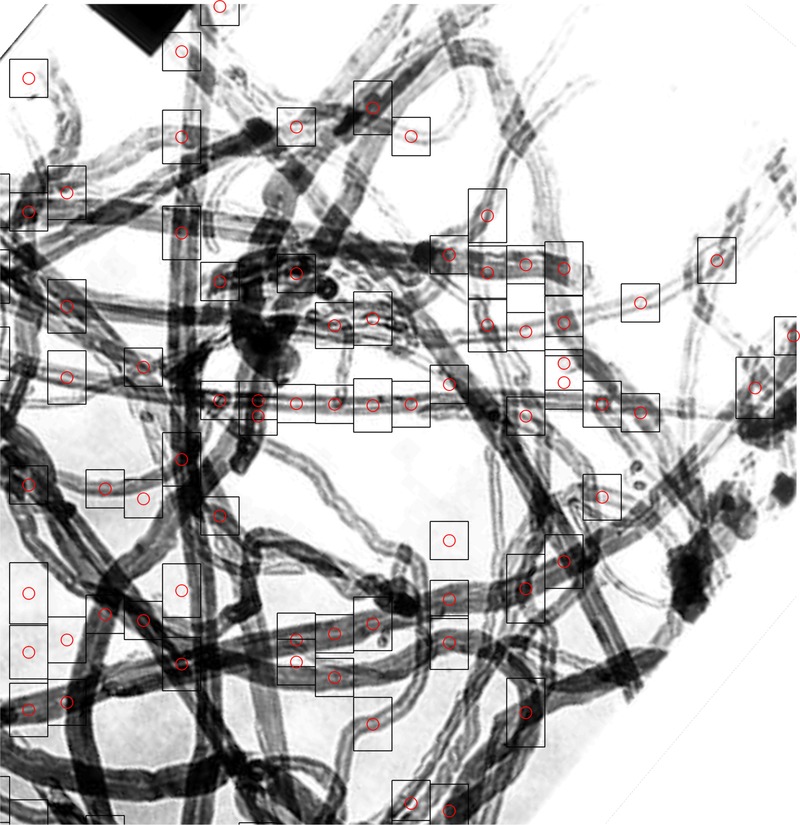	Automatic detection of carbon nanotubes - image processing (SEMIE 2016, Grenoble)
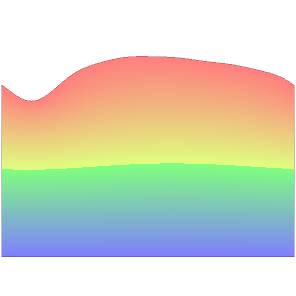	Critical waves using a shape optimization approach
	Min-max optimal partitions for Dirichlet eigenvalues
	Maximization of the first Dirichlet Laplace eigenvalue on domains with holes
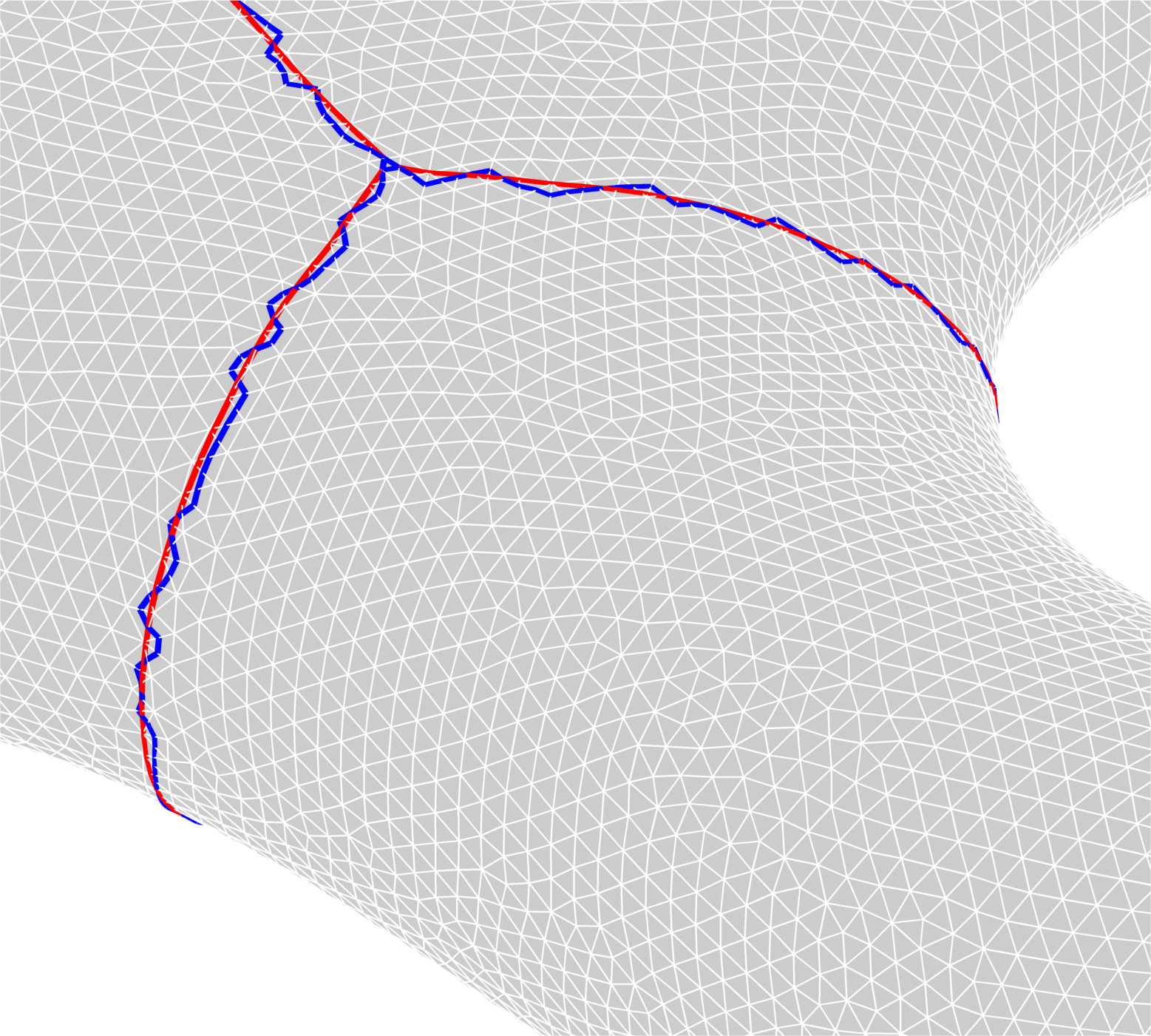	Contour smoothing on triangulations - minimization of perimeter - area constraints
	Large spectral partitions
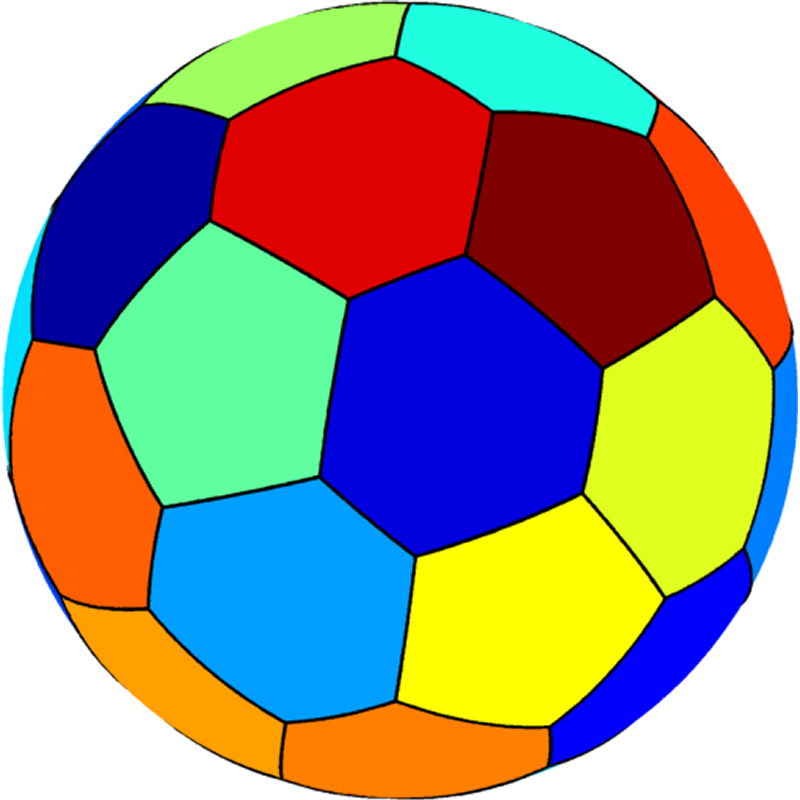	Optimal spectral partitions on the sphere
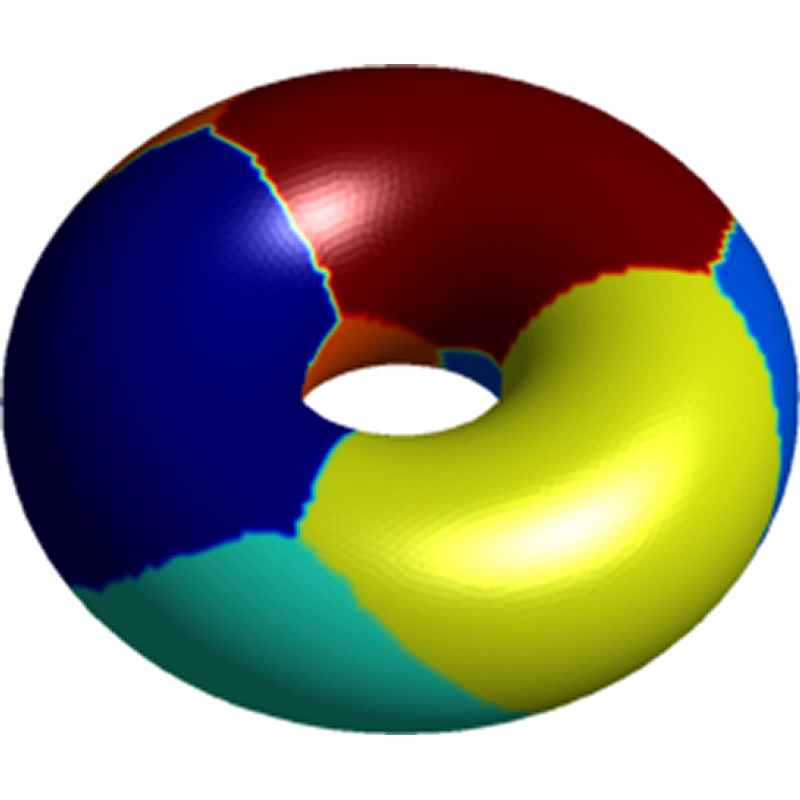	Perimeter minimizing equi-areal partitions on surfaces
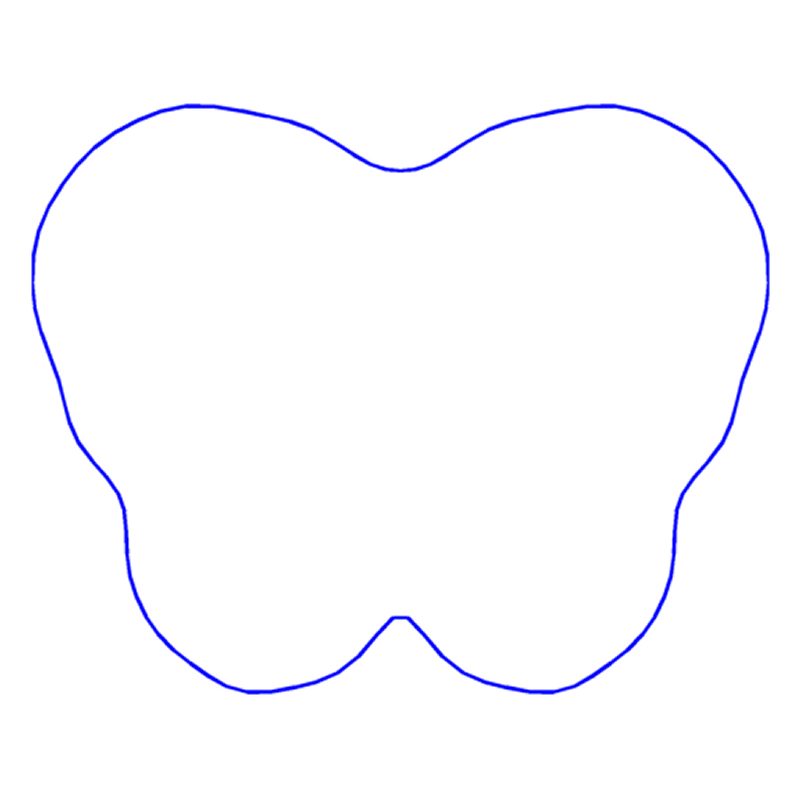	Optimizing Dirichlet Laplace eigenvalues - volume constraint in 2D ($k \leq 21$)
	Optimizing Dirichlet Laplace eigenvalues - perimeter constraint in 2D ($k \leq 50$)
	Optimizing Dirichlet Laplace eigenvalues - perimeter constraint - $\Gamma$-convergence method 2D and 3D
	Optimization of functionals depending on the Steklov spectrum
	Numerical method based on fundamental solutions - computation Steklov spectrum
	Minimal spectral partitions on 2D regions
	Numerical computations for the multiphase problem $\min \left( \sum_{i=1}^h \lambda_k(\Omega_i)+m|\Omega_i|\right)$
	Numerical testing for Polya's conjecture - $N \in [5,15]$
	Numerical optimal partitions for anisotropic perimeters using $\Gamma$-convergence
	Numerical minimal equal area partitions on general regions using $\Gamma$-convergence
	The basic idea behind numerical methods based on $\Gamma$-convergence. Numerical example: the isoperimetric problem.