Software

Below you can find a few algorithms I implemented. If you find some of the codes below useful and you use them in your research, please give credit by citing a related publication.

Computing Blaschke Santalo diagrams using Centroidal Voronoi Tessellations: Github repository. The codes correspond to the following paper.

Numerical Shape Optimization among Convex Sets: Github repository. The codes correspond to the following paper.

Longest Minimal Length Partitions: Github repository. The codes correspond to the following paper.

Computation of the Steklov/Wentzell Spectrum using FreeFem

The following program computes the first few eigenvalues of the Steklov/Wentzell operator for a two dimensional shape. The current shape is quite particular, but it can be changed by using any of the methods available in FreeFem for defining boundaries. This code was used in my article concerning the computation of the Wentzell spectrum with fundamental solutions in order to compare my results to the ones obtained with a mesh-based method. You can download the FreeFem program here: wentzel_test.edp (right click, Save as).

The Steklov/Wentzell Spectrum using fundamental solutions in Matlab

The following algorithm uses fundamental solutions in order to solve certain spectral problems. The method was inspired by Alves and Antunes and it is presented in detail in this publication. You can get the program here: wentzell_test.m (right click, Save as) You could check out the huge speed difference between this fundamental solution formulation and the FreeFem code.

Dirichlet eigenvalue optimization in 2D with FreeFem

The following algorithm is an example of eigenvalue shape optimization problem under area constraint in two dimensions. It uses finite element computations in FreeFem. This type of numerical computations were initially performed by E. Oudet and recently by P. Antunes and P. Freitas. I revisited them using Mpspack in my phd thesis. The following program works rather well for the first 10 eigenvalues. Sometimes different initial conditions should be used to get close to the minimizer. You can get the program here: dirichlet_low10.edp (right click, Save as).

Maximization of the fundamental eigenvalue in domains with holes - FreeFem code

We want to find the position of some circular holes in a two dimensional domain which maximize the first Dirichlet Laplace eigenvalue. More details about the problem and the results you can obtain using the algorithm can be found here. The FreeFem code is available here: optimal_holes.edp (right click, Save as).

Numerical study of Polya's conjecture with FreeFem

The following script starts from a polygon and evolves using the gradient flow given by the derivative of the first Dirichlet eigenvalue under area constraint. We can see that the algorithm converges towards a regular polygon, which is to be expected, since Polya's conjecture suggests that regular polygons minimize the first Dirichlet Laplace eigenvalue under area constraint. More details about the problem and the algorithm can be found here. The FreeFem code is available here: Polya_flow.edp (right click, Save as).

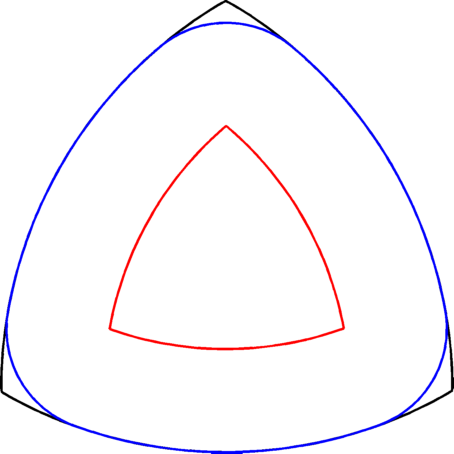
Computation of Cheeger sets for polygons - Matlab

This algorithm combines a well known result of Kawohl and Lachand-Robert which characterizes the Cheeger sets for convex domains and the toolbox Clipper, a very good implementation of polygon offset computation by Agnus Johnson. For the algorithm to work you'll need to install the toolbox New Polygon Clipping and Offsetting by Erik Johnson. Once you've installed it, things should run smoothly. Check out the examples to find how the algorithm works.

This algorithm was implemented to test the performance of a relaxation by $\Gamma$-convergence proposed in a recent article in collaboration with Dorin Bucur and Ilaria Fragala. Details can be found here. The algorithm together with the $\Gamma$-convergence variant can be found at the following GitHub repository: Cheeger_patch.

Accurate computation of eigenvalues for spherical triangles and application to the study of 3D random walks

Please refer to this page for codes and details regarding the paper 3D positive lattice walks and spherical triangles.

The numerical codes contain the following:

a method for computing eigenvalues for spherical triangles using finite elements. The classical finite elements method has convergence of order 2. Using an extrapolation procedure we observe a rate of convergence of at least 6 and we are able to get close to machine precision for cases which interest us.
Other codes deal with the study of critical exponents for some random walks. The search for these exponents has a few steps: search for the global minimum of an inventory function using a Newton method, finding the associated spherical triangle and computing its eigenvalue.

Make $\LaTeX$ like drawings with Metapost

If you are use to typewriting in $\LaTeX$ then you may find working in Metapost a pleasant experience. It allows you to code an image and to obtain a vectorized result (that is, something that is still sharp even when zooming). You may find nice tutorials on the internet, for example here and here.

What I find most useful is to start from an example and slowly build my figure. That's why I share on this page some of my figures and the code used to generate them.

In order to compile metapost you can either use the command mptopdf in linux or use the online compiler by Troy Henderson. The examples on the web are png and are not lossless. If you use mptopdf you will obtain vectorized pdfs which can be then included in Latex documents.

Disclaimer: these software programs are provided "as is", without any warranty of any kind... The author cannot be held responsible for any misuse of these programs or any damage that may come from using them.

Useful computing software

Here are some Matlab toolboxes I use a lot:

LBFGS by Liam Stewart: a nice implementation of the LBFGS optimization algorithm. It allows bounds on every variable and the use of callback functions.
minFunc by Mark Schmidt. Minfunc allows the use of many types of optimization algorithms like steepest descent lbfgs, etc.
minConf by Mark Schmidt. It is a variant of minFunc where you can also put constraints. Way faster than Matlab's fmincon, even faster than the LBFGS wrapper by Lian Stewart linked above (at least for the test cases I tried).
HANSO: BGFS optimization implementation.
MpsPack. A Matlab toolbox which solves all sorts of problems from PDE to eigenvalue problems. It uses methods based on particular solutions. It is rather fast and very precise.

Although I'm not a specialist, I find FreeFem++ to be really useful in the study of PDEs. It has all you need to get you started, and all the dirty work regarding meshes is done automatically once you give it the right commands. There's a really nice visual editor for FreeFem++, which makes the installation and use of FreeFem programs very easy. You can find it here: freefem++cs

Project Euler stats

Created Jun 2015. Last modified: Apr 2017