Algèbre max-plus : Une approche géométrique.
Algèbre max-plus : Une approche géométrique.
Edouard Wagneur
L'algèbre max-plus sur les réels (auxquels on adjoint le point -infini)
détermine un demi-anneau idempotent 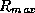 . Nnous avons proposé d'appeler
pseudomodule la structure de semimodule idempotent sur ce demi-anneau.
Dans cette algèbre, les équations d'évolution d'un SDED sont linéaires
et du type
. Nnous avons proposé d'appeler
pseudomodule la structure de semimodule idempotent sur ce demi-anneau.
Dans cette algèbre, les équations d'évolution d'un SDED sont linéaires
et du type 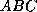 . Plus précisement, nous avons des équations de la forme
. Plus précisement, nous avons des équations de la forme
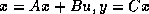 .
Dans
.
Dans 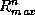 , les conditions de résolution de cette equation sont liées
au problème d'accessibilité et sont telles qu'il appara^it
necessaire d'étudier, en toute généralité, les classes
d'équivalence des objets de la forme
, les conditions de résolution de cette equation sont liées
au problème d'accessibilité et sont telles qu'il appara^it
necessaire d'étudier, en toute généralité, les classes
d'équivalence des objets de la forme 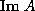 , où
, où 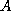 est une application (max-linéaire) de
est une application (max-linéaire) de 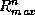 dans
dans 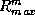 .
Ceci nous amène à introduire le concept de torsion dans un pseudomodule,
qui se distingue du concept de torsion dans un module par le fait qu'il est
ici fortement lié à la structure d'ordre associée à la structure
`linéaire'. Nous obtenons alors un théorème de décomposition, qui est
l'analogue du théorème classique de décomposition d'un module en partie
libre et partie de torsion.
.
Ceci nous amène à introduire le concept de torsion dans un pseudomodule,
qui se distingue du concept de torsion dans un module par le fait qu'il est
ici fortement lié à la structure d'ordre associée à la structure
`linéaire'. Nous obtenons alors un théorème de décomposition, qui est
l'analogue du théorème classique de décomposition d'un module en partie
libre et partie de torsion.
Nous verrons aussi comment le concept de suite exacte
courte :
(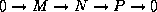 ),familier en théorie des groupes
abéliens et des modules classiques
peut être généralisé aux pseudomodules.
),familier en théorie des groupes
abéliens et des modules classiques
peut être généralisé aux pseudomodules.
Tue May 28 18:12:54 MET DST 1996
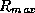 . Nnous avons proposé d'appeler
pseudomodule la structure de semimodule idempotent sur ce demi-anneau.
Dans cette algèbre, les équations d'évolution d'un SDED sont linéaires
et du type
. Nnous avons proposé d'appeler
pseudomodule la structure de semimodule idempotent sur ce demi-anneau.
Dans cette algèbre, les équations d'évolution d'un SDED sont linéaires
et du type 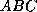 . Plus précisement, nous avons des équations de la forme
. Plus précisement, nous avons des équations de la forme
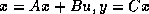 .
Dans
.
Dans 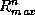 , les conditions de résolution de cette equation sont liées
au problème d'accessibilité et sont telles qu'il appara^it
necessaire d'étudier, en toute généralité, les classes
d'équivalence des objets de la forme
, les conditions de résolution de cette equation sont liées
au problème d'accessibilité et sont telles qu'il appara^it
necessaire d'étudier, en toute généralité, les classes
d'équivalence des objets de la forme 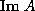 , où
, où 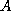 est une application (max-linéaire) de
est une application (max-linéaire) de 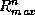 dans
dans 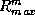 .
Ceci nous amène à introduire le concept de torsion dans un pseudomodule,
qui se distingue du concept de torsion dans un module par le fait qu'il est
ici fortement lié à la structure d'ordre associée à la structure
`linéaire'. Nous obtenons alors un théorème de décomposition, qui est
l'analogue du théorème classique de décomposition d'un module en partie
libre et partie de torsion.
.
Ceci nous amène à introduire le concept de torsion dans un pseudomodule,
qui se distingue du concept de torsion dans un module par le fait qu'il est
ici fortement lié à la structure d'ordre associée à la structure
`linéaire'. Nous obtenons alors un théorème de décomposition, qui est
l'analogue du théorème classique de décomposition d'un module en partie
libre et partie de torsion.
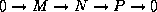 ),familier en théorie des groupes
abéliens et des modules classiques
peut être généralisé aux pseudomodules.
),familier en théorie des groupes
abéliens et des modules classiques
peut être généralisé aux pseudomodules.