A Generalized Markov-Chain Modelling Approach to (1,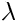)-ES Linear Optimization

Alexandre Chotard¹ and Martin Holea²

¹INRIA Saclay-Ile-de-France, LRI, University Paris-Sud, France
alexandre.chotard@lri.fr

²Institute of Computer Science, Academy of Sciences, Pod vodárenskou ví 2, Prague, Czech Republic
martin@cs.cas.cz

Abstract. Several recent publications investigated Markov-chain modelling of linear optimization by a (1,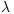)-ES, considering both unconstrained and linearly constrained optimization, and both constant and varying step size. All of them assume normality of the involved random steps, and while this is consistent with a black-box scenario, information on the function to be optimized (e.g. separability) may be exploited by the use of another distribution. The objective of our contribution is to complement previous studies realized with normal steps, and to give sufficient conditions on the distribution of the random steps for the success of a constant step-size (1,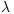)-ES on the simple problem of a linear function with a linear constraint. The decomposition of a multidimensional distribution into its marginals and the copula combining them is applied to the new distributional assumptions, particular attention being paid to distributions with Archimedean copulas.

Keywords: Evolution strategies, continuous optimization, linear optimization, linear constraint, linear function, Markov chain models, Archimedean copulas

LNCS 8672, p. 902 ff.

Full article in PDF | BibTeX

lncs@springer.com
© Springer International Publishing Switzerland 2014