Maximizing Submodular Functions under Matroid Constraints by Multi-objective Evolutionary Algorithms

Tobias Friedrich¹ and Frank Neumann²

¹Friedrich-Schiller-Universität Jena, 07743, Jena, Germany

²Optimisation and Logistics, School of Computer Science, The University of Adelaide, Adelaide, SA 5005, Australia

Abstract. Many combinatorial optimization problems have underlying goal functions that are submodular. The classical goal is to find a good solution for a given submodular function f under a given set of constraints. In this paper, we investigate the runtime of a multi-objective evolutionary algorithm called GSEMO until it has obtained a good approximation for submodular functions. For the case of monotone submodular functions and uniform cardinality constraints we show that GSEMO achieves a (1 – 1/e)-approximation in expected time 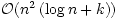, where k is the value of the given constraint. For the case of non-monotone submodular functions with k matroid intersection constraints, we show that GSEMO achieves a 1/(k + 2 + 1/k + 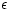)-approximation in expected time .

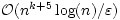LNCS 8672, p. 922 ff.

Full article in PDF | BibTeX

lncs@springer.com
© Springer International Publishing Switzerland 2014