A multiphase eigenvalue problem - numerical computations
This work was inspired from the article Multiphase
shape optimization problems by D. Bucur and B. Velichkov. The authors
consider the optimization of multiphase functionals for eigenvalue
problems. One particular case is the problem
$$ \min \left(\sum_{i=1}^h \lambda_1(\Omega_h)+m|\Omega_h|\right), \hspace{2cm} (M)$$
where $\Omega_i$ are disjoint and contained in a bounded open set $D$.
The case $m=0$ was studied in a previous work
of D. Bucur, B. Bourdin and
E. Oudet. If $m=0$ then $(\Omega_i)$ form a partition of $D$. The numerical
computations suggest that, asymptotically, the optimal configuration consists of a regular
hexagon tiling.
In the case $m>0$ the authors give some
interesting qualitative results concerning the optimal configuration, among
which they prove that there are no triple junction points, i.e $\partial \Omega_i \cap
\partial \Omega_j \cap \partial \Omega_k =\emptyset$ for different $
i,j,k$. This motivated us to try and see if we could reproduce numerically
this phenomenon. Below I present some results obtained for different
values of $m$ in the non-periodic case. It turns out that non only there
do not exist triple points corresponding to the phases, but the same
behavior happens near the boundary. This motivated us to search for a proof
of this fact, and this can be found in my joint article with B. Velichkov,
which can be found here.
Let $D\subset\Bbb{R}^2$ be a bounded open set with Lipschitz boundary
$\partial D$. Let $(\Omega_1,\dots,\Omega_h)$ be optimal for
the multiphase problem $(M)$. Then for any pair of distinct indexes
$i,j\in\{1,\dots,h\}$, we have that $\partial\Omega_i\cap\partial
\Omega_j\cap\partial D=\emptyset$.
 |
 |
 |
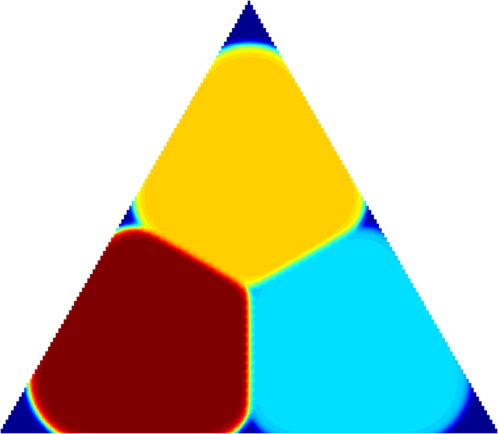
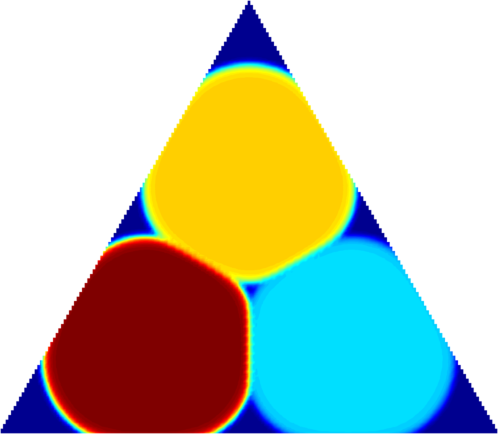
| $3$ phases, $m=170$ |
$3$ phases, $m=100$ |
$3$ phases, $m=80$ |
 |
 |
 |
| $4$ phases, $m=250$ |
$4$ phases, $m=150$ |
$4$ phases, $m=100$ |
In the non-periodic case, we can see a resemblance
with the case $m=0$. For small values of $m$, the configuration resembles
a hexagonal partition with small holes near triple points. As $m$ increases,
the cells tend to distribute uniformly, as can be seen in the picture with
the pentagonal configuration.
 |
 |
 |
| $8$ phases, $m=500$ |
$8$ phases, $m=580$ |
$8$ phases, $k=2$, $m=270$ |
We noticed an interesting behavior in the periodic case. If we consider a domain
which can be partitioned in regular hexagons, and we look for various values of
the parameter $m$, we notice that the shapes in the optimal configuration
seem to be congruent and monotonically decreasing with respect to $m$. This
fact suggests that the multiphase problem we consider seems to connect
the well known circle packing problem with the unsolved conjecture that the spectral
optimal tiling of the plane is made of regular hexagons. In the figures below you
can notice this monotonic behavior with respect to $m$.
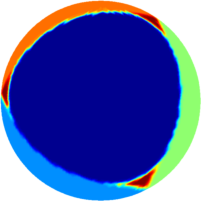
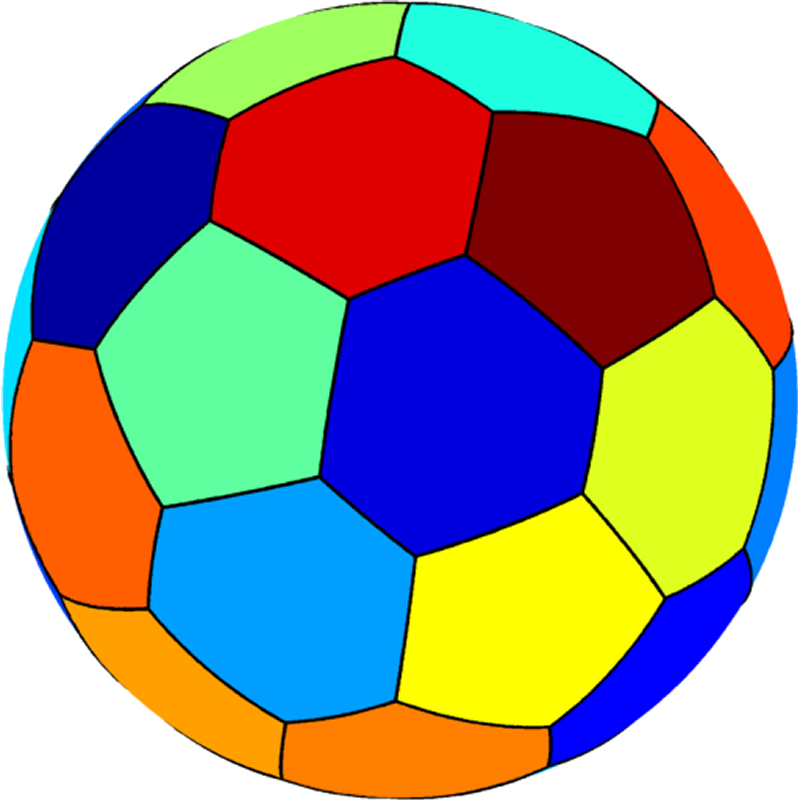
We were able to extend the numerical framework to three dimensional surfaces, using
the same methods presented
here. We notice
the same monotonic behavior. Below you can see optimal configurations on the sphere
for various values of the parameter $m$. If the monotonicity property is true
then this would lead to an answer to some open problems concerning the
spectral optimal partitions on the sphere in the cases corresponding to regular
polyhedra.
Created: Dec 2014