Emmanuel GOBET - Images
-
Valuation of an American Put (optimal stopping problem),
using an optimization of the exercice boundary.
Based on the boundary sensitivity formula from Boundary
sensitivities for diffusion processes in time
dependent domains (C. Costantini, E. Gobet and N. El
Karoui), Applied
Mathematics
and Optimization, Vol.54(2), pp.159-187, 2006.
|
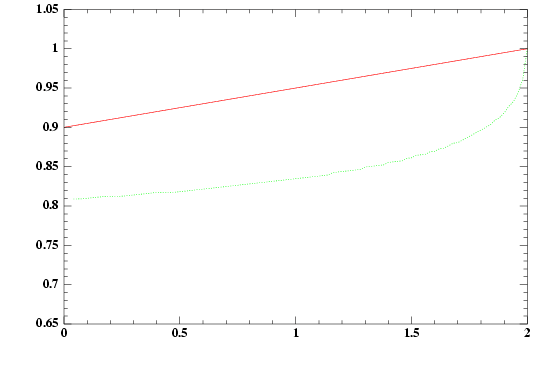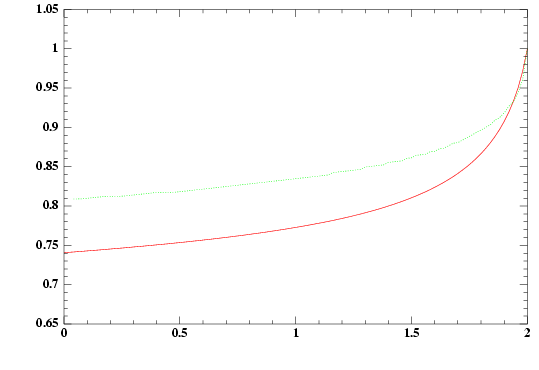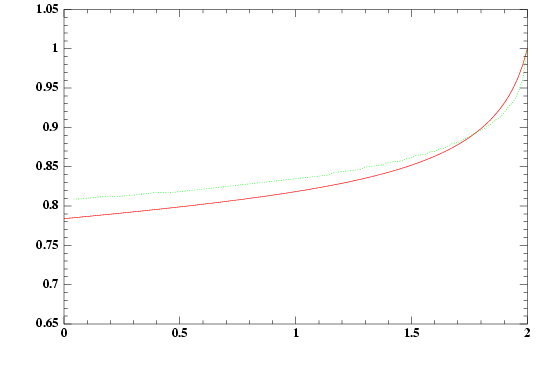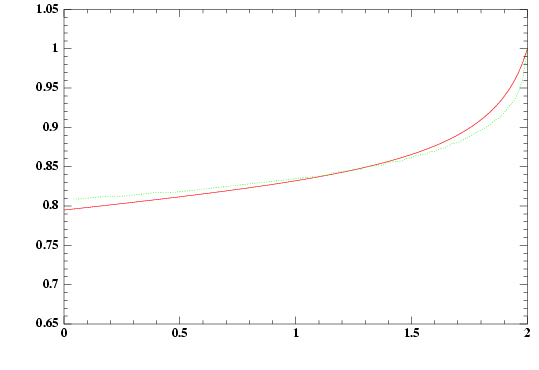
Green: the optimal
boundary.
Red: the iterative
approximation.
Axis: x for time, y for space.
(Reload to get the boundary animation). |
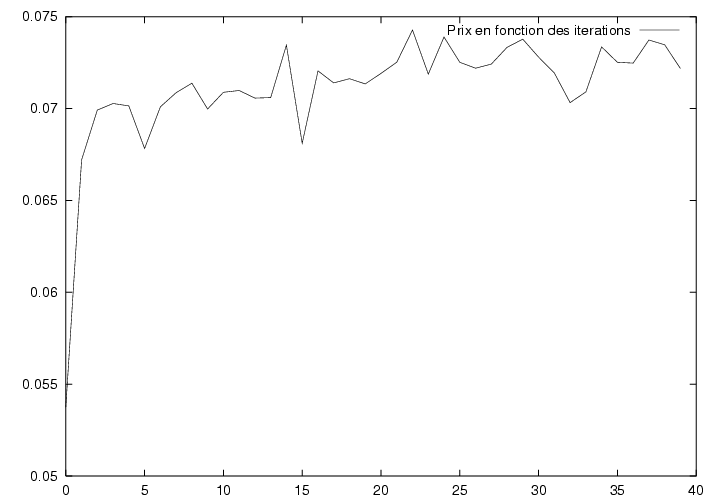
|
Convergence of the value function (put price) through
iterations. |
-
Convergence of policy value iteration in 4-d dimensional
stochastic control problem.
Example from Sensitivity analysis using Itô-Malliavin calculus
and martingales. Application to stochastic optimal control
(E. Gobet and R. Munos),
SIAM Journal on Control and Optimization, Vol.43(5),
pp.1676-1713, 2005.
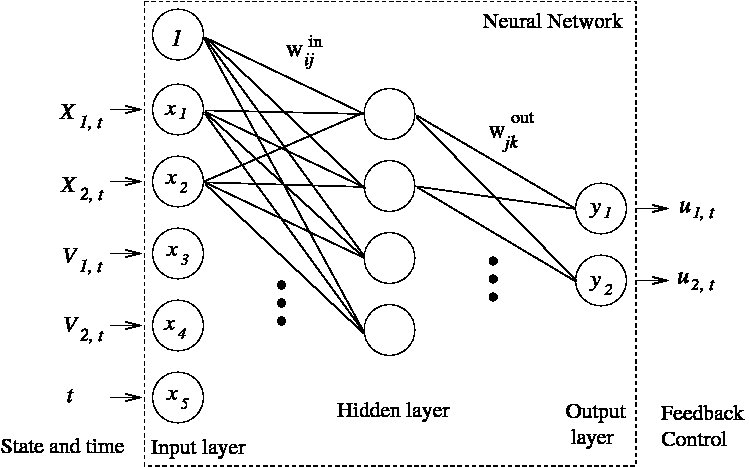
|
The neural network to approximate the policy as a
function of time and space. |
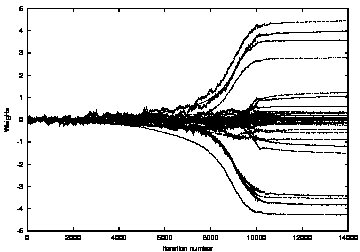
|
The evolution of the neural network parameters through
the stochastic optimization algorithm. |
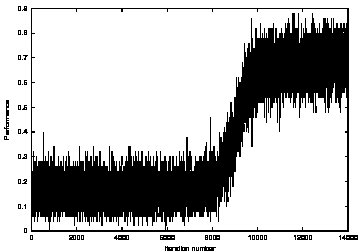
|
Performance of the algorithm (maximization of a
probability of reaching a stochastic fly). |
-
Geometric convergence of the adaptive control variates
algotithm.
Based on
|
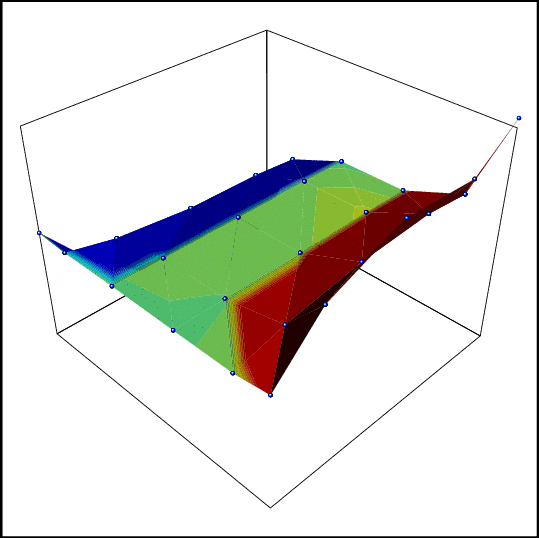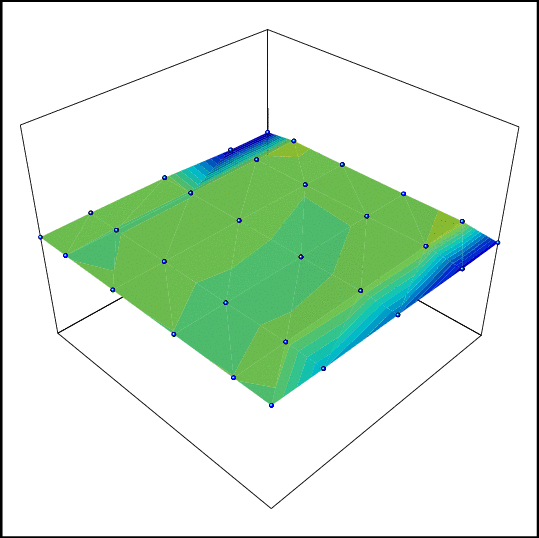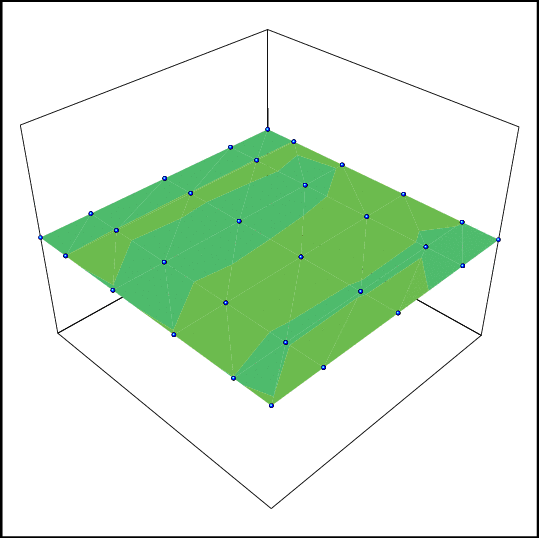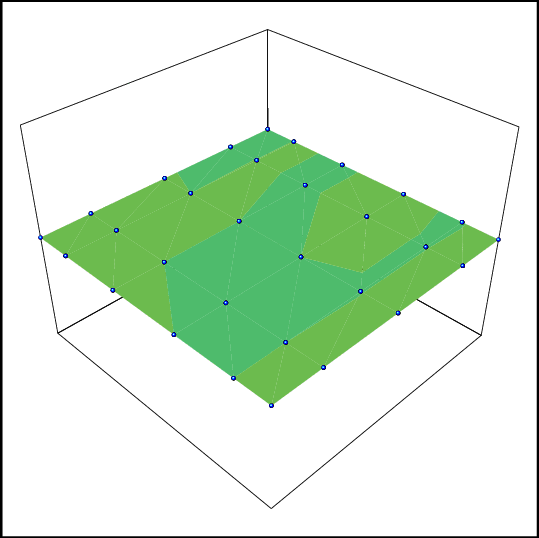
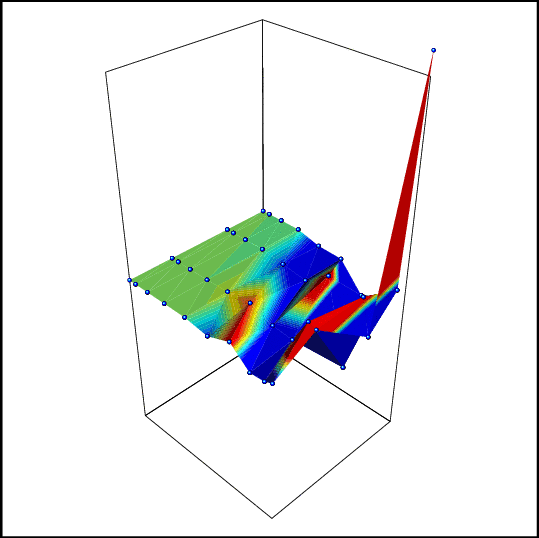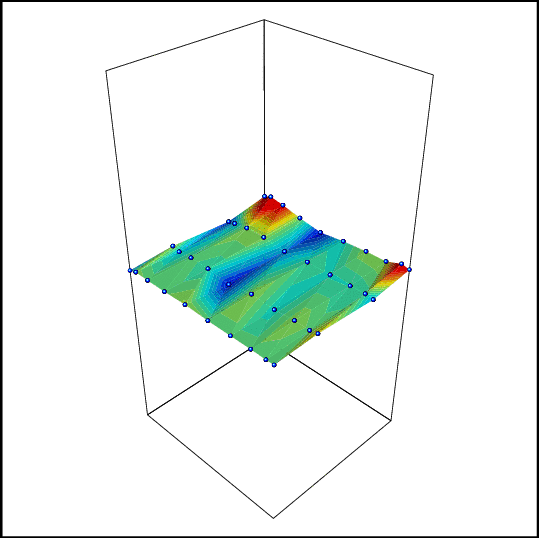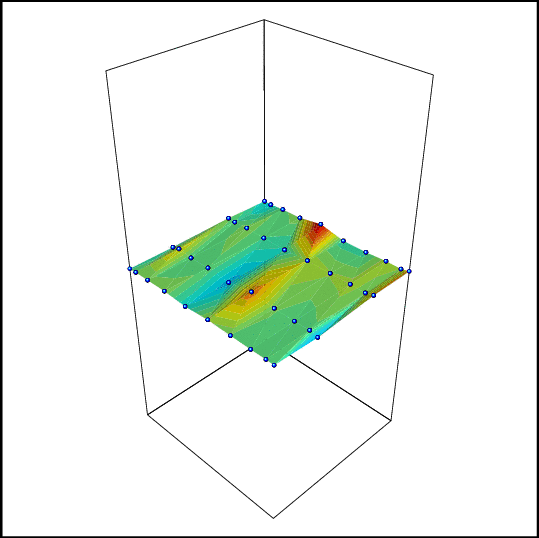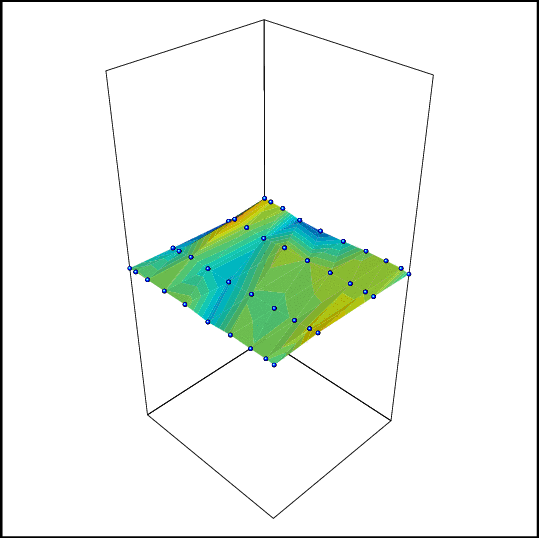
2-d
example, convergence of the error to 0, using only 2 (!!)
simulations
at each point of the grid. The solution is polynomial and
polynomial
interpolation is used to approximate the solutions. Each
image
corresponds to a new iteration (Reload to get the
animation). |
|
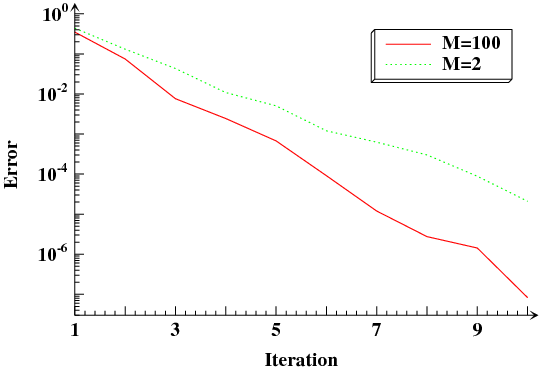
Comparison of the geometric convergence using 2 or 100
simulations. |
|
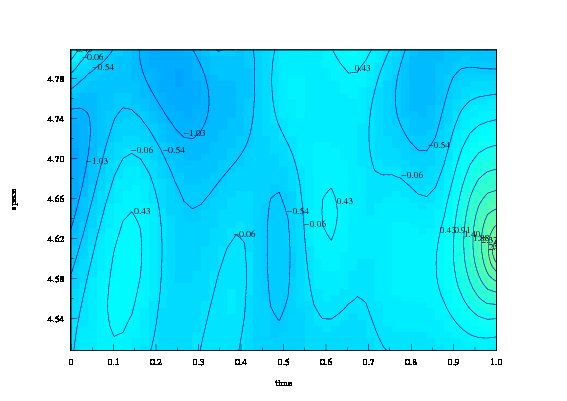
Performance of the algorithm when the solution is not
polynomial and
polynomial interpolation is used (Reload to get the
animation). |
|
The same type of algorithm is now designed and tested on
Backward
Stochastic Differential Equations (associated to
semi-linear PDE). Here
is the convergence for call payoff and linear driver.
Axis: x for space and y for time. The errors are larger
close to the singularity (2,1) (i.e. the strike). |
-
Boundary shifting to compensate overestimation of exit times.
Based on
- Stopped diffusion processes: overshoots and boundary
correction (E. Gobet and S. Menozzi), Stochastic
Processes and their Applications, Vol.120, pp.130-162,
2010.
- Advanced Monte Carlo methods for barrier and related
exotic options
(E. Gobet), Handbook of Numerical Analysis, Vol. XV. Elsevier.
Special
Volume: Mathematical Modeling and Numerical Methods in
Finance. Editor:
P.G. Ciarlet. Guest Editors: Alain Bensoussan and Qiang Zhang.
pp.497-528, 2009.
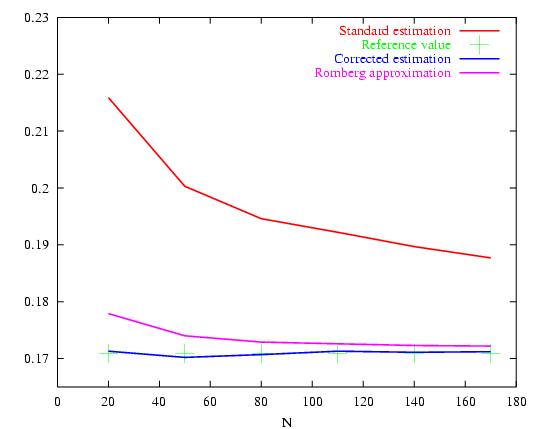
|
Convergence
comparison between the standard method (discrete exit time
in Red),
Romberg extrapolation (pink) and the boundary correction
method (blue).
The advantage of the Boundary correction method over
Brownian bridge
techniques is its avalaibility in any dimension. |
COPYRIGHT 2009, 2010.
CMAP UMR 7641 Ecole Polytechnique and CNRS, Institut Polytechnique de Paris, Route de Saclay, 91128 Palaiseau Cedex France










