 |
    |
Unbiased Black-Box Complexity of Parallel Search
Golnaz Badkobeh1, Per Kristian Lehre2, and Dirk Sudholt1
1University of Sheffield, UK
2University of Nottingham, UK
Abstract. We propose a new black-box complexity model for search algorithms evaluating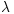 
search points in parallel. The parallel unbiased black-box complexity gives lower bounds on the number of function evaluations every parallel unbiased black-box algorithm needs to optimise a given problem. It captures the inertia caused by offspring populations in evolutionary algorithms and the total computational effort in parallel metaheuristics. Our model applies to all unary variation operators such as mutation or local search. We present lower bounds for the LeadingOnes function and general lower bound for all functions with a unique optimum that depend on the problem size and the degree of parallelism, 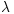. The latter is tight for OneMax; we prove that a (1+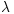) EA with adaptive mutation rates is an optimal parallel unbiased black-box algorithm.
LNCS 8672, p. 892 ff.
lncs@springer.com
© Springer International Publishing Switzerland 2014