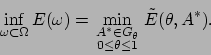Comme on l'a déjà dit dans l'introduction, il est maintenant bien
connu (depuis les premiers contre-exemples de [23] et les
constatations numériques de [13]), qu'en l'absence de
contraintes supplémentaires sur les formes admissibles ![]() , la
fonction objectif
, la
fonction objectif ![]() peut ne pas atteindre son minimum,
c'est-à-dire qu'il n'existe pas de forme optimale. La raison mécanique
de ce phénomène générique de non-existence est qu'il est souvent
avantageux de faire beaucoup de très petits trous (plutôt que quelques
grand trous) dans une structure donnée afin d'améliorer sa performance
par rapport à la fonction
peut ne pas atteindre son minimum,
c'est-à-dire qu'il n'existe pas de forme optimale. La raison mécanique
de ce phénomène générique de non-existence est qu'il est souvent
avantageux de faire beaucoup de très petits trous (plutôt que quelques
grand trous) dans une structure donnée afin d'améliorer sa performance
par rapport à la fonction ![]() . Par conséquent, atteindre le
minimum peut faire appel à un processus de passage à la limite
(lorsque les trous deviennent de plus en plus petits et de plus en plus
nombreux) conduisant à une forme ``généralisée''
(ou homogénéisée) qui est un matériau composite obtenu par
microperforation du matériau élastique d'origine.
. Par conséquent, atteindre le
minimum peut faire appel à un processus de passage à la limite
(lorsque les trous deviennent de plus en plus petits et de plus en plus
nombreux) conduisant à une forme ``généralisée''
(ou homogénéisée) qui est un matériau composite obtenu par
microperforation du matériau élastique d'origine.
Afin de prendre en compte ce phénomène mécanique d'optimalité
qui n'est pas réalisée par une forme, stricto sensu, mais par un
matériau composite, nous devons élargir l'espace des formes admissibles
en autorisant, dès le départ, les matériaux composites obtenus par
homogénéisation d'un mélange fin du matériau et de vide. Une telle
structure composite est déterminée par deux fonctions: ![]() , sa
densité volumique locale de matériau (prenant ses valeurs entre
, sa
densité volumique locale de matériau (prenant ses valeurs entre ![]() et
et
![]() ), et
), et ![]() , sa loi de Hooke effective correspondant à sa
microstructure. Bien entendu, il faut aussi trouver une définition
adéquate de la fonction objective homogénéisée
, sa loi de Hooke effective correspondant à sa
microstructure. Bien entendu, il faut aussi trouver une définition
adéquate de la fonction objective homogénéisée
![]() qui généralise
qui généralise ![]() pour ces structures
composites.
pour ces structures
composites.
Ce procédé de généralisation des formes admissibles est appelé relaxation, ou, dans ce cas particulier, homogénéisation. Il est essentiel de noter que cette relaxation ne change pas la physique du problème. En effet, une forme optimale composite est simplement une moyenne (ou une équivalence en un certain sens) de formes classiques proches de l'optimalité. Mathématiquement, une forme composite optimale n'est que la limite au sens de l'homogénéisation d'une suite minimisante de formes classiques. Intrinsèquement, le problème d'optimisation de formes n'est donc pas modifié. En particulier, toute solution possible du problème original est aussi solution du problème homogénéisé. Pour calculer cette formulation relaxée ou homogénéisée de l'optimisation de formes, on fait appel à la théorie de l'homogénéisation (voir par exemple [10], [28]). L'objectif final est double : d'une part prouver un résultat d'existence pour la formulation relaxée du problème d'optimisation de forme, et d'autre part trouver un nouvel algorithme numérique pour le calcul des formes optimales.
L'utilisation de l'homogénéisation dans ce contexte est assez technique
(notamment à cause de la dégénérescence du problème causée par
la présence de trous), et nous nous contentons de donner le résultat
obtenu (pour plus de détails voir [3], [4]). On note
![]() l'ensemble de toutes les lois de Hooke
correspondant à des matériaux composites de densité
l'ensemble de toutes les lois de Hooke
correspondant à des matériaux composites de densité ![]() , c'est-à-dire
obtenus en perforant le matériau original
, c'est-à-dire
obtenus en perforant le matériau original ![]() par des trous en proportions
par des trous en proportions
![]() . La fonctionnelle homogénéisée ou relaxée est alors donnée par
. La fonctionnelle homogénéisée ou relaxée est alors donnée par
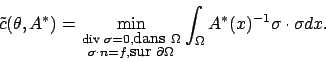 |
(7) |
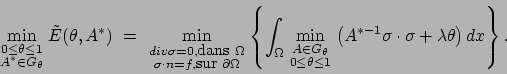
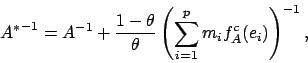
 |
Après cette étape cruciale, la minimisation par rapport
à la densité ![]() est aisément faite à la main, ce qui
termine le calcul explicite des paramètres de la forme composite
optimale pour un tenseur de contraintes donné
est aisément faite à la main, ce qui
termine le calcul explicite des paramètres de la forme composite
optimale pour un tenseur de contraintes donné ![]() . Citons
simplement pour l'exemple la valeur optimale de la densité en
2-D
. Citons
simplement pour l'exemple la valeur optimale de la densité en
2-D
Théorème
La formulation homogénéisée (6) est la
relaxation du problème d'optimisation de formes (4)
au sens où, (i) il existe, au moins, une forme optimale composite
![]() qui minimise (6), (ii) toute suite
minimisante de formes classiques
qui minimise (6), (ii) toute suite
minimisante de formes classiques ![]() pour (4) converge,
au sens de l'homogénéisation, vers un minimisateur
pour (4) converge,
au sens de l'homogénéisation, vers un minimisateur ![]() de
(6), (iii) les valeurs des minima de l'énergie
originale et homogénéisée coincident
de
(6), (iii) les valeurs des minima de l'énergie
originale et homogénéisée coincident