Beniamin BOGOSEL
Partitions minimizing the sum of eigenvalues in 3D
The goal is to find numerically partitions which minimize the sum of the first eigenvalues of the Dirichlet Laplace operator: $$ \min_{(\omega_i)} \lambda_1(\omega_1)+...+\lambda_1(\omega_n).$$ where $(\omega_i)$ is a partition of a three dimensional shape $D$. The objective is to apply the (already classical) penalization method used by Bourdin, Bucur and Oudet here. The main difficulty in the application of the same methods is the sheer size of the computations involved.
Things become more simple if we use an approach similar to the one presented here. Dealing with partitions is simpler if we keep a fixed grid. Then the eigenvalue of each cell is computed by solving a problem on the entire grid. This can be costly from a computational point of view. Instead of using the whole grid for every cell we may just localize the grid around each cell and ignore other points. This grid restriction algorithm was already used successfully in 2D and on surfaces in 3D here.
This is a work in progress. I'll update the page as soon as new results or presentation updates appear. For now here are a few initial results.
If you keep the mouse on pictures you can see a detailed view of the rotating partition. Due to the size of the images it may take a while to load, so put the mouse on the image you want to see and wait a bit.
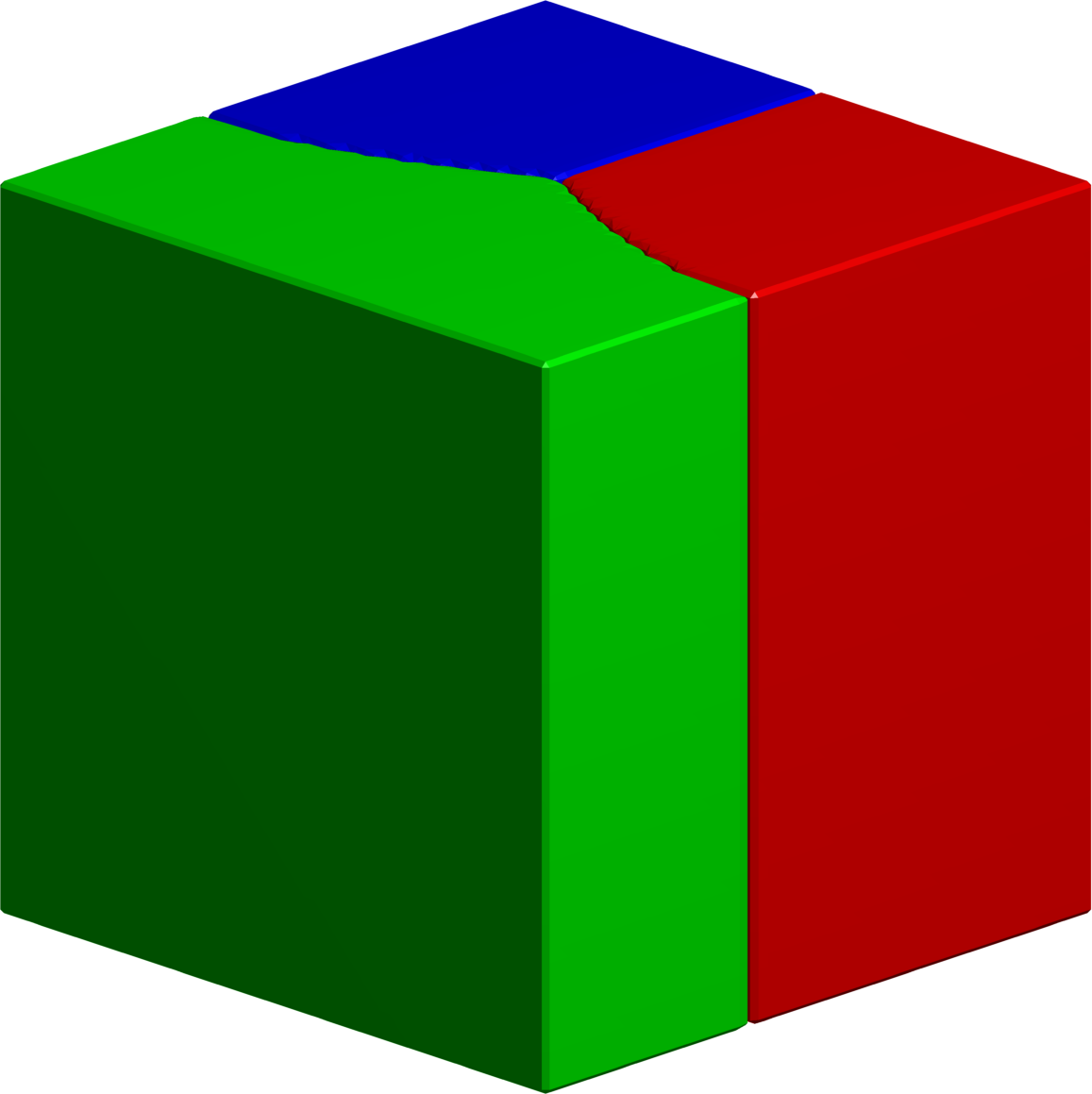
$3$-partition of the cube
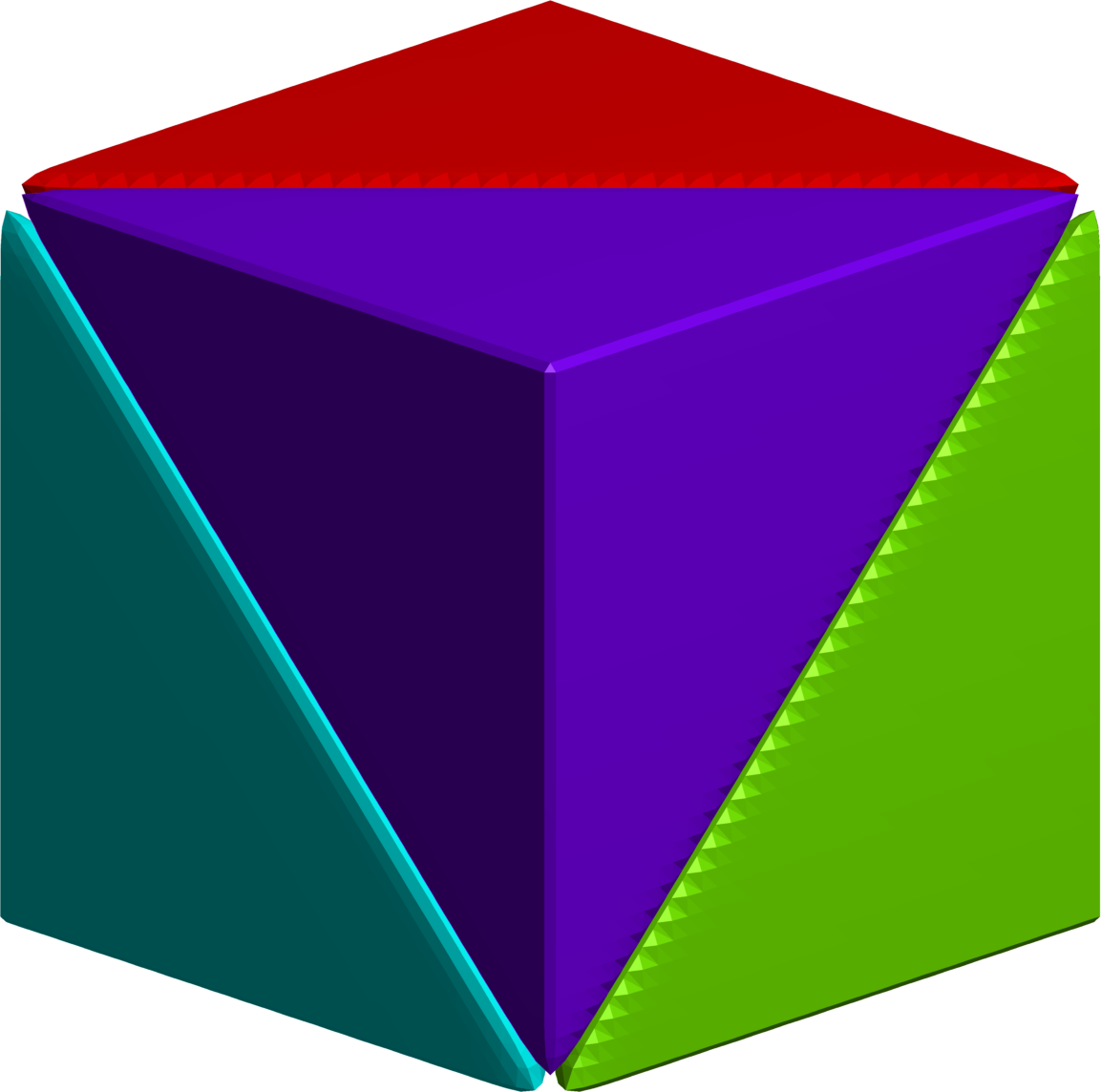
$4$-partition of the cube
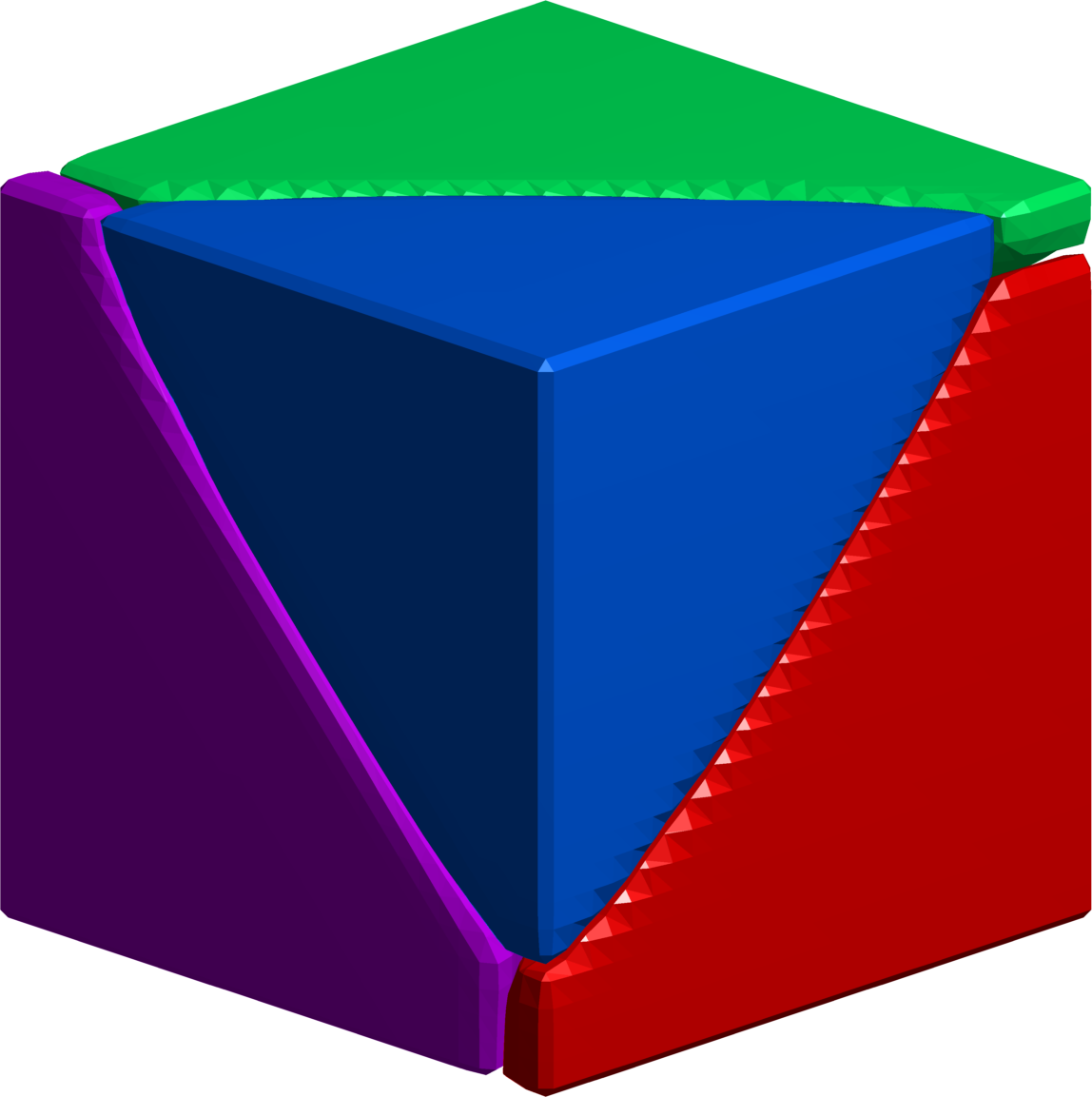
$5$-partition of the cube
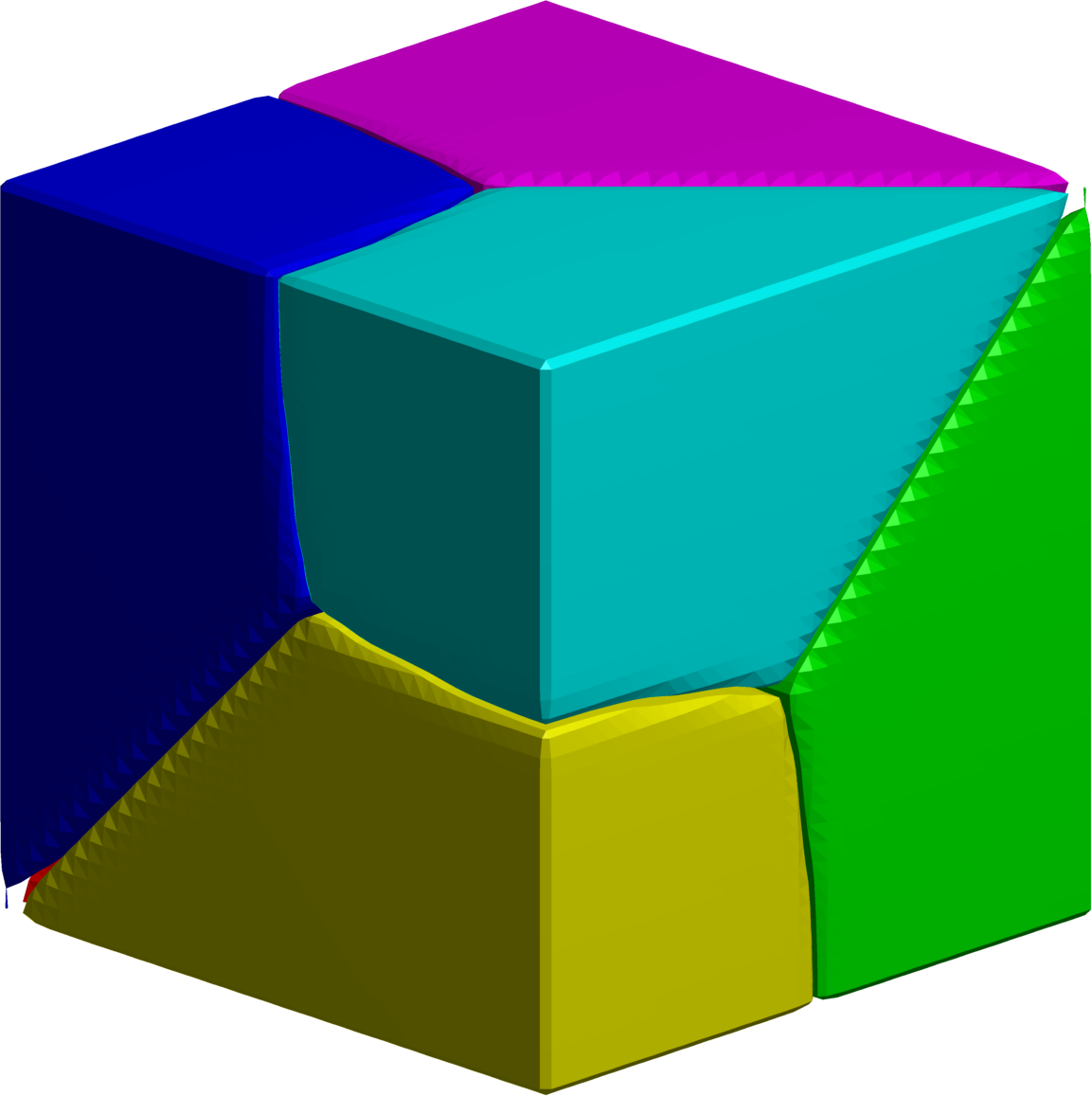
$6$-partition of the cube

$8$-partition of the cube

$9$-partition of the cube
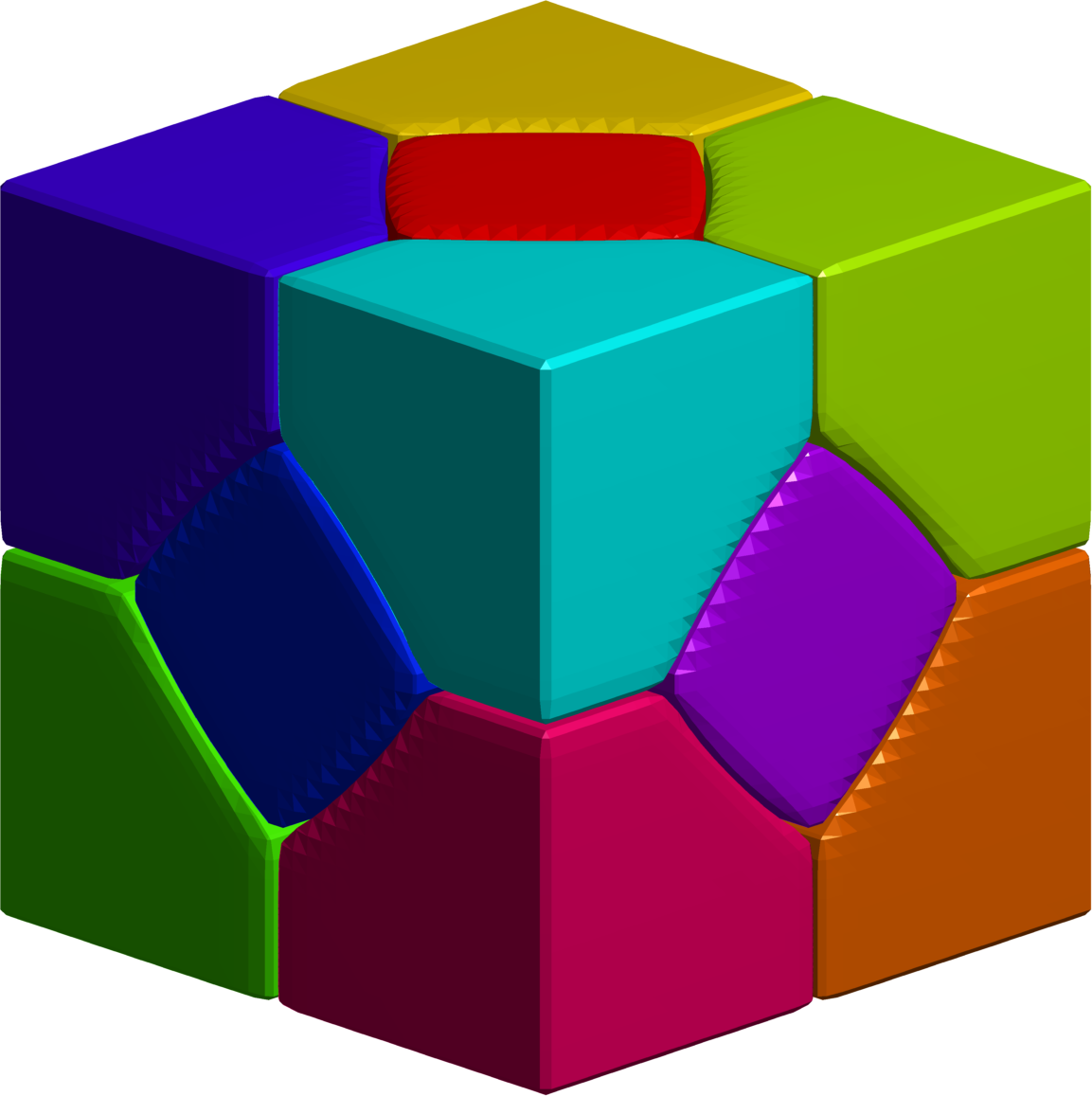
$14$-partition of the cube
And now some results in the periodic case.

$16$-partition of the cube. The Kelvin structure: truncated octahedra
Below are some computations for the case of the sphere and the regular tetrahedron.
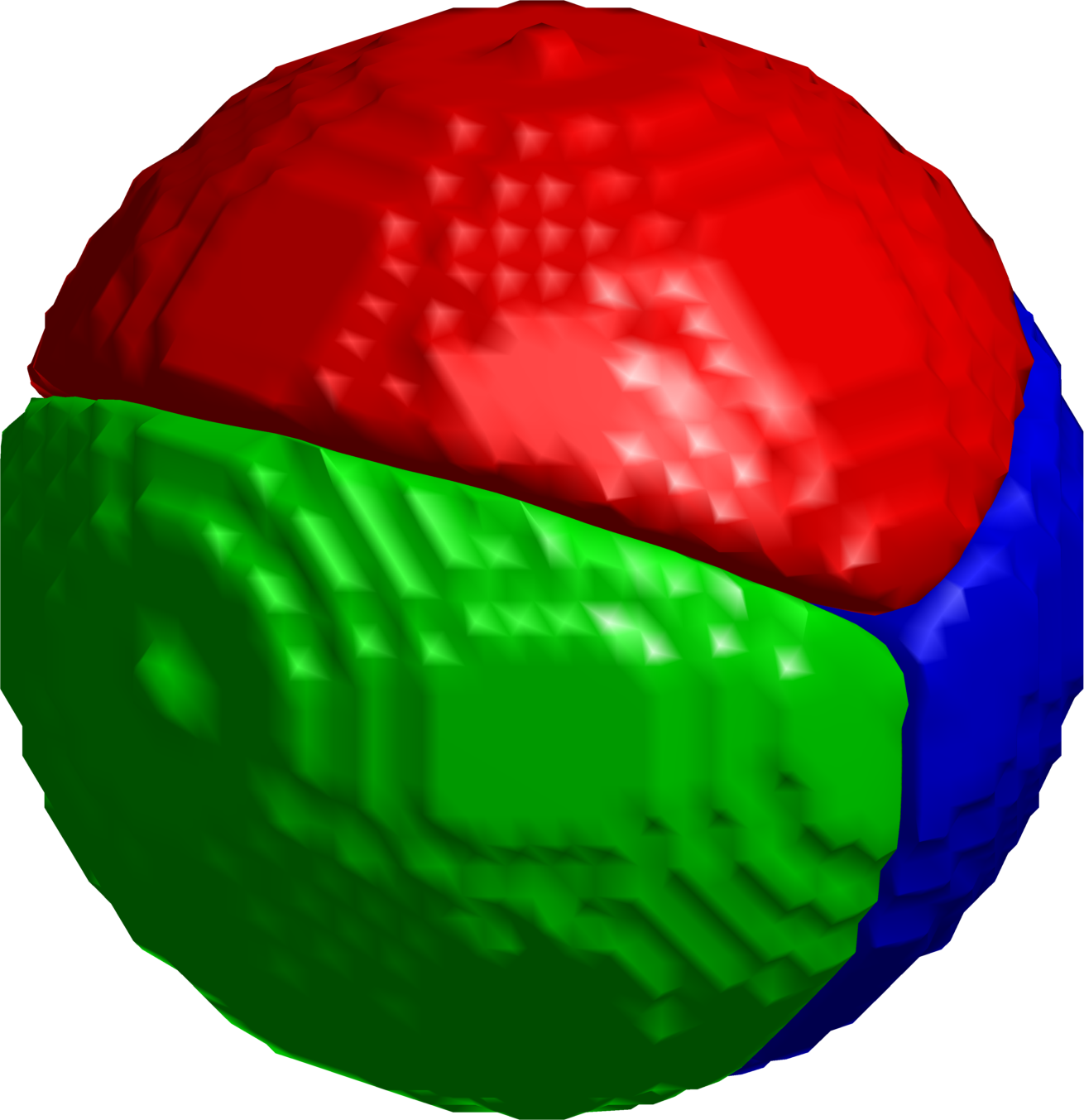
$3$-partition on the sphere.
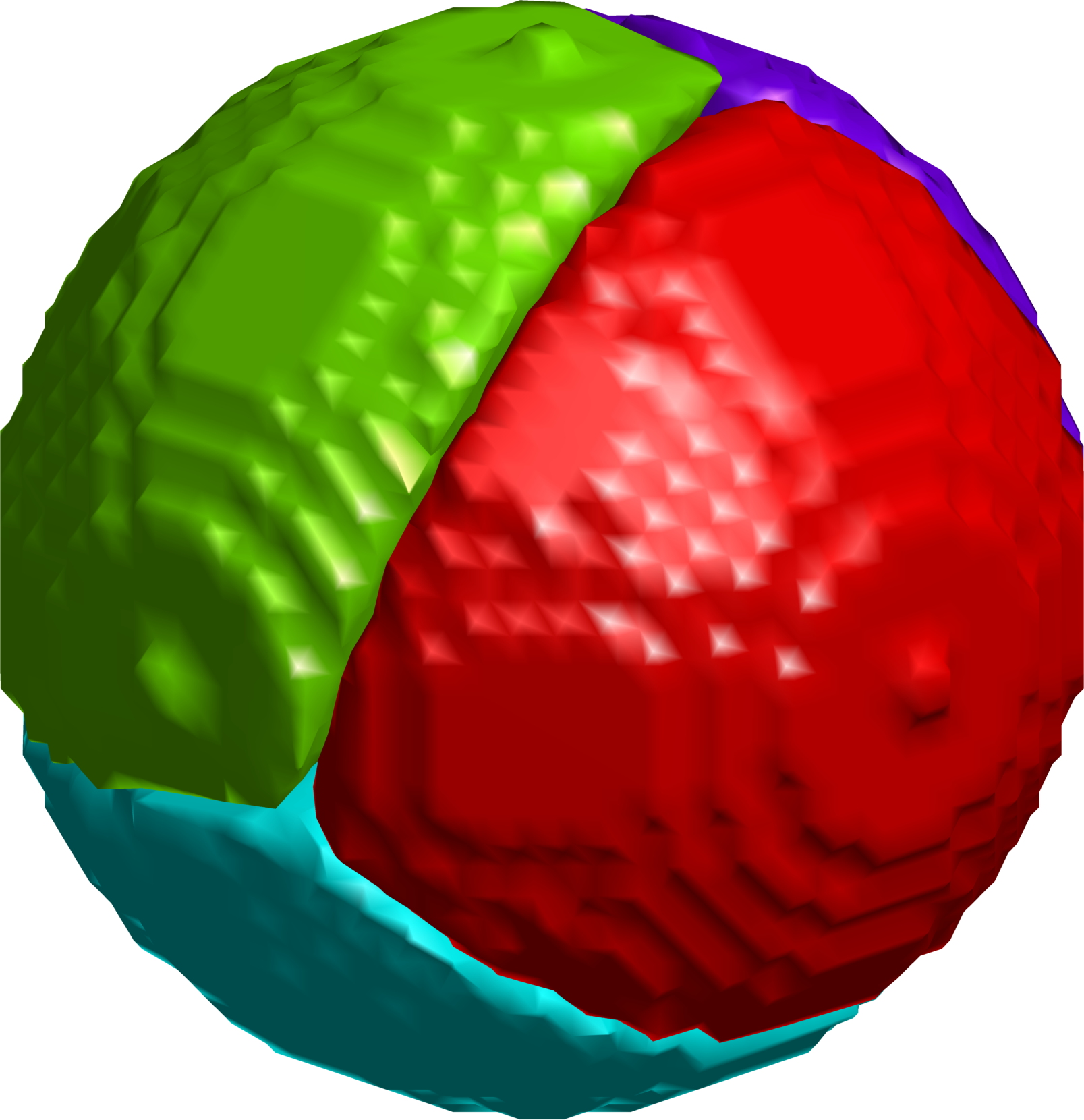
$4$-partition on the sphere.
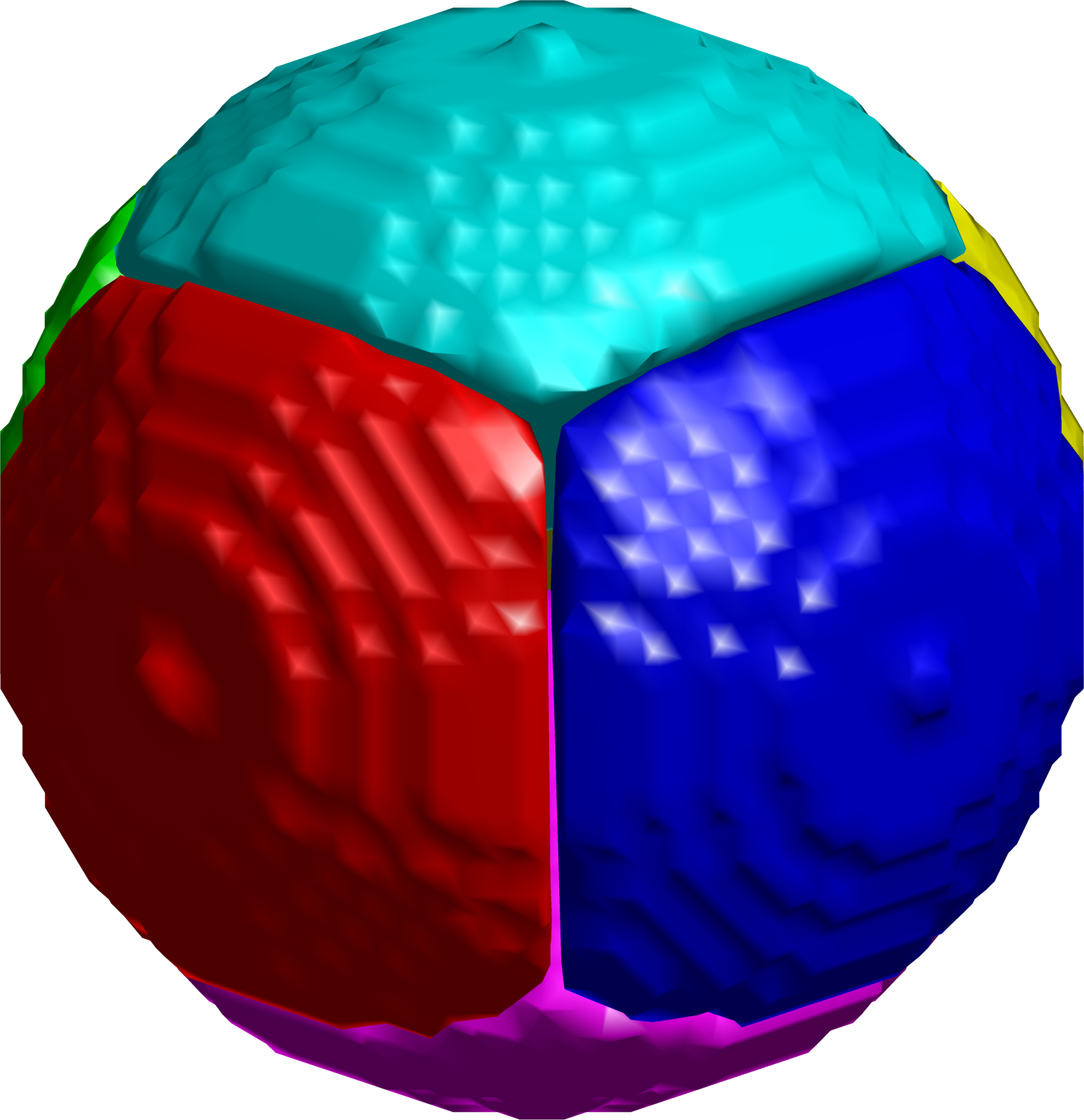
$6$-partition on the sphere.
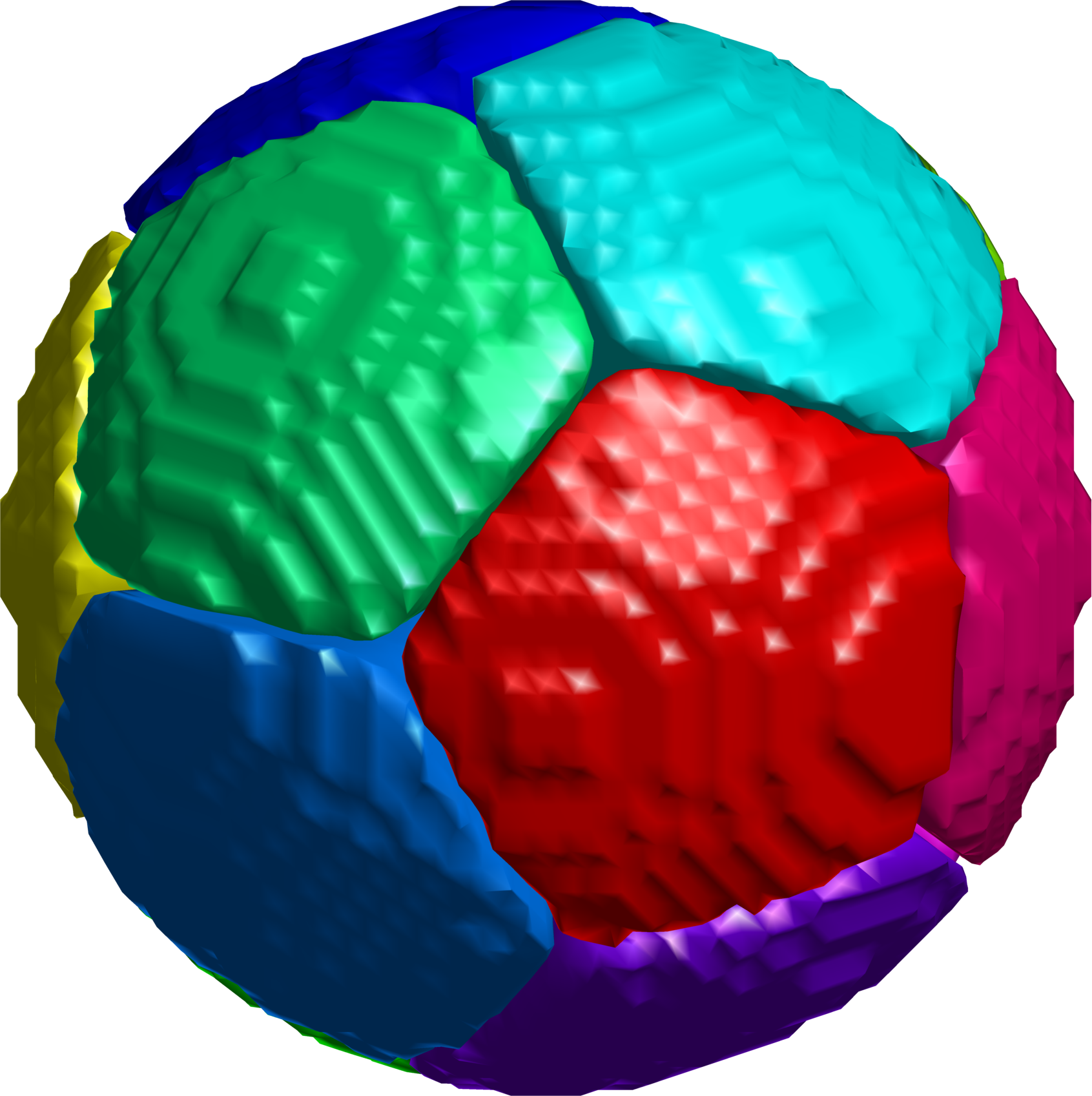
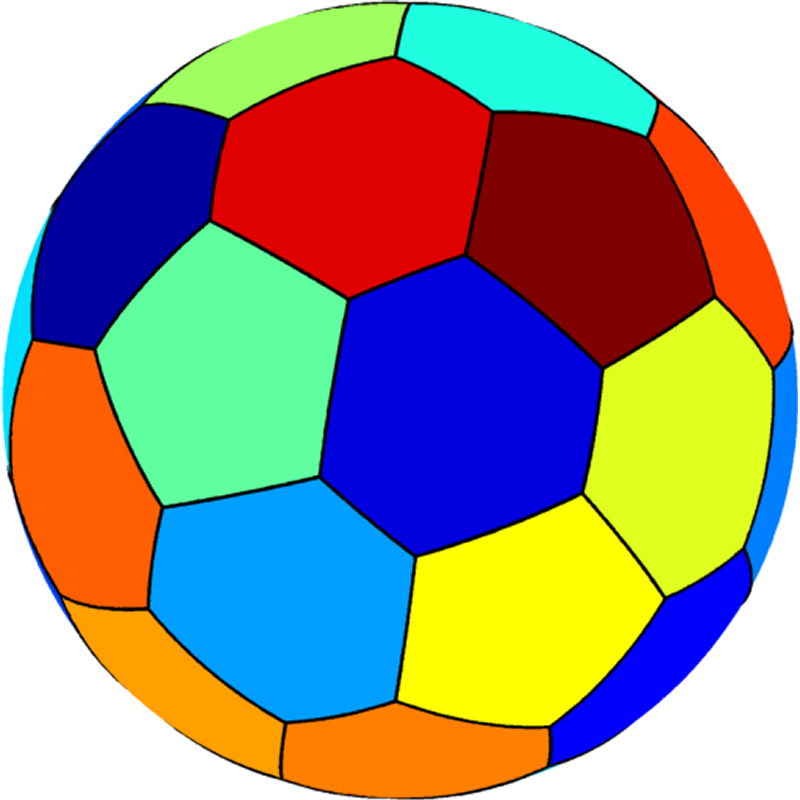
$12$-partition on the sphere.

$13$-partition on the sphere.

$2$-partition on the tetrahedron.
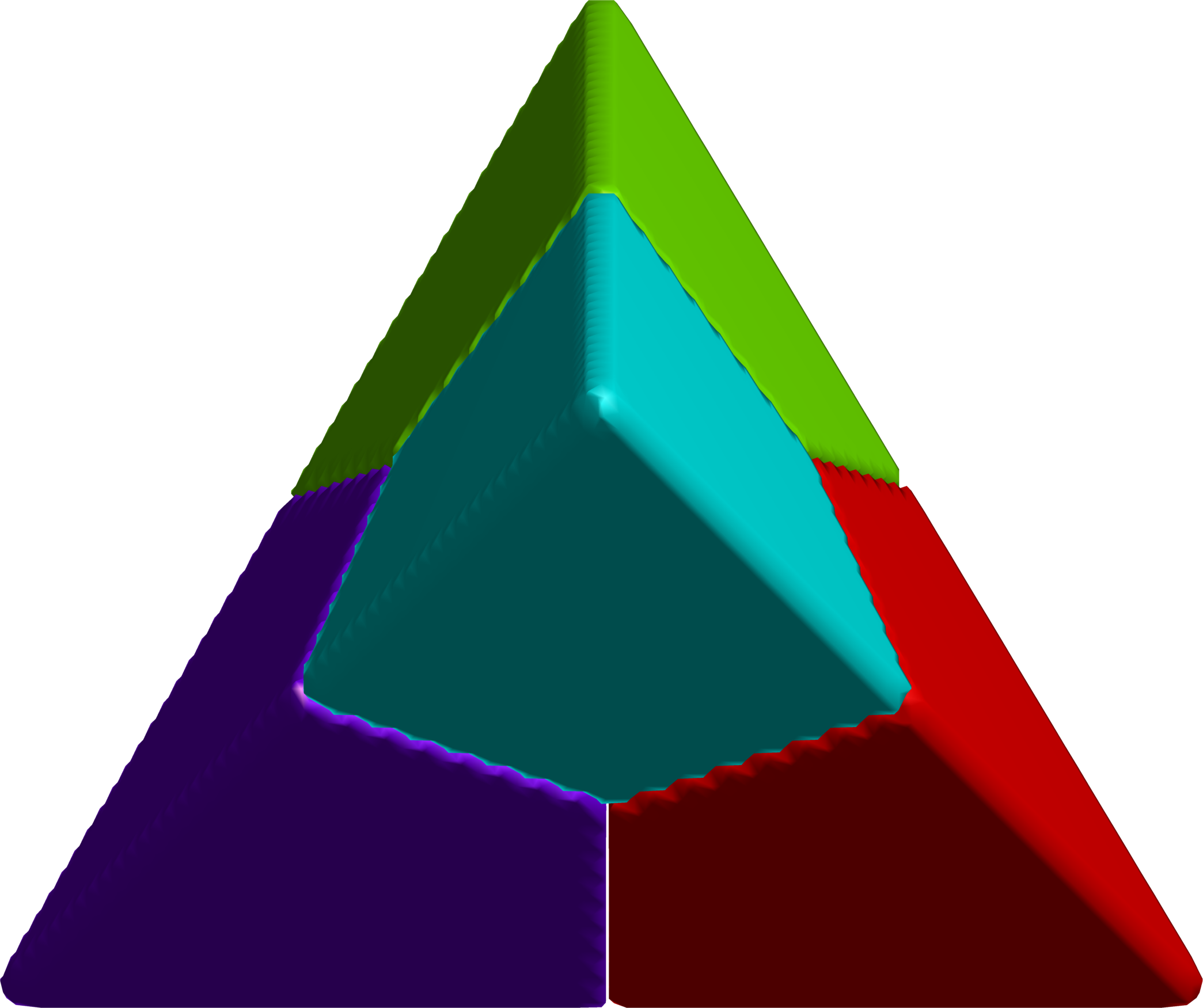
$4$-partition on the tetrahedron.
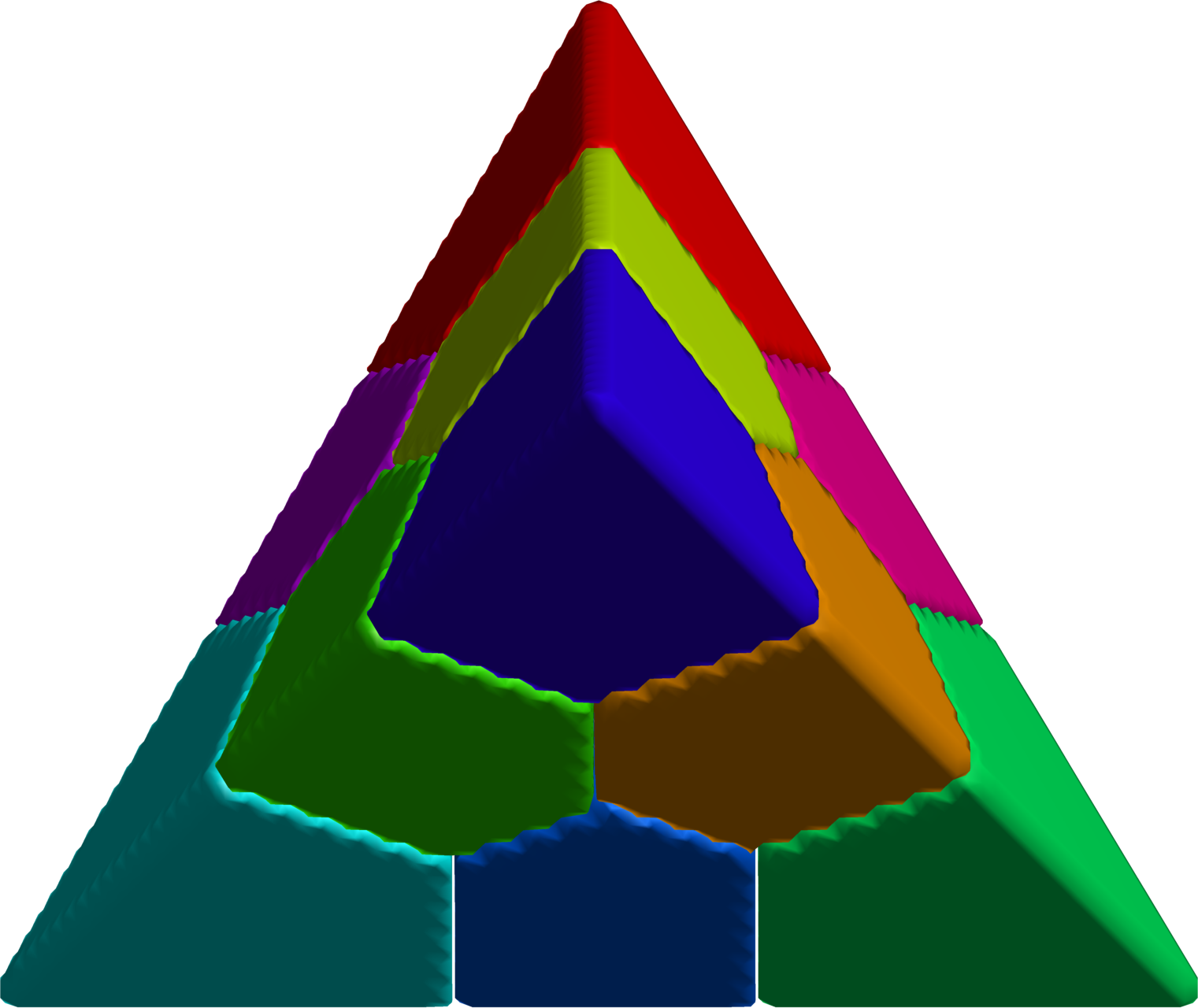
$10$-partition on the tetrahedron.
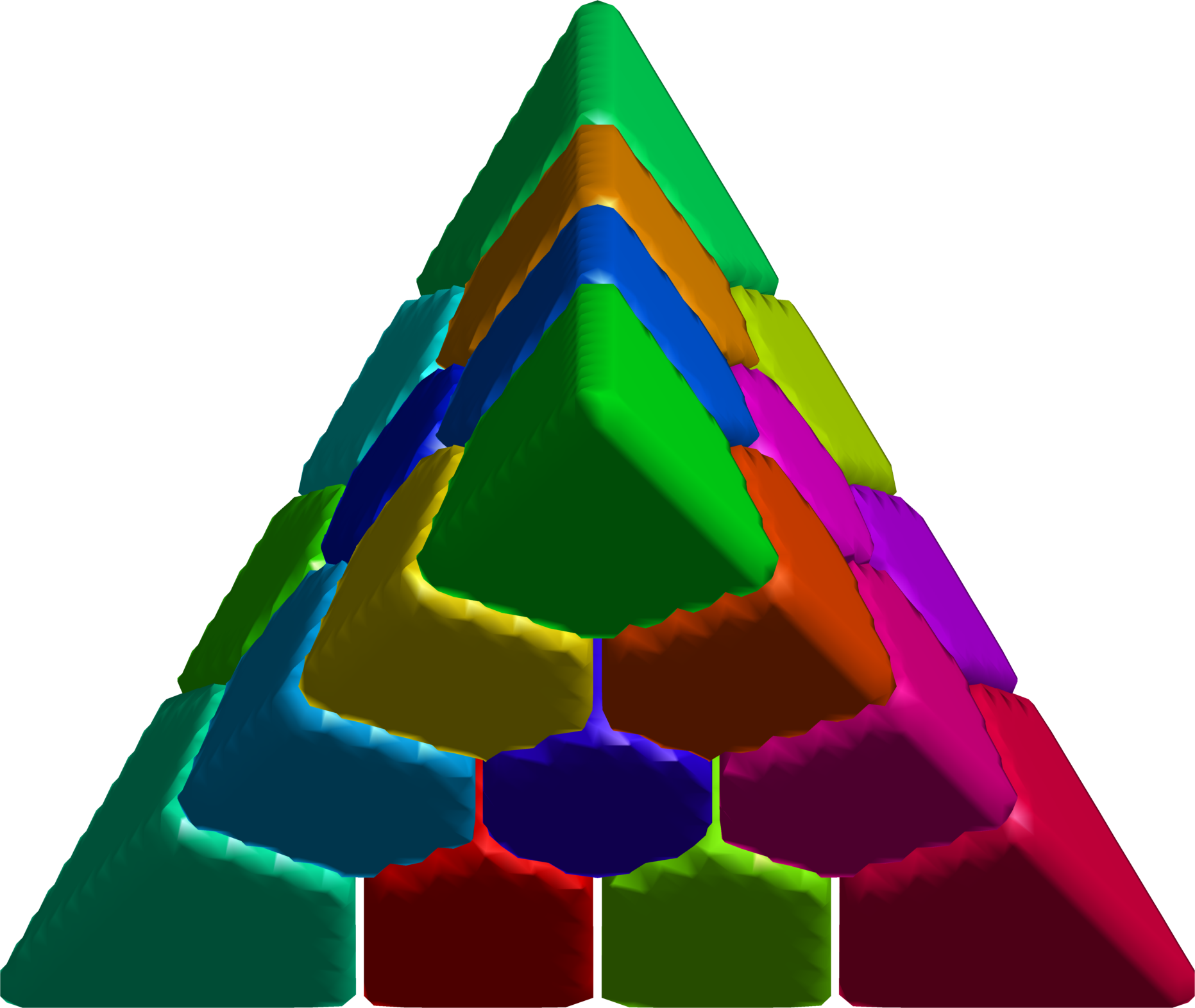
$20$-partition on the tetrahedron.
Created: Nov 2016