Spectral optimal partitions on surfaces

These computations are presented in my paper: "The method of fundamental solutions applied to boundary eigenvalue problems". You can consult a set of results for other surfaces by clicking here.

Here are some preliminary numerical results for a problem of optimal partitioning on the sphere. We consider the problem $$ \min \sum_{i=1}^n \lambda_1^{LB}(S_i)$$ where $(S_i)$ is a partition of the sphere into $n$ parts. The same problem was studied recently by Elliott and Ranner (link), using a different numerical method.

The computations made below were made using a method based on fundamental solutions (inspired from the one mentioned here). The numerical optimization is made in two steps:

Both of the above steps are based on the same method of fundamental solutions.

We present below the numerical results we obtained for $3 \leq n \leq 17$ and $n=32$ parts (the goal is to make the computations for all $k \in [3,32]$. Our results coincide with those of Elliott and Ranner, which made computations for $n \in \{3,4,5,6,7,8,16,32\}$. The case $n=12$ was not considered in their article, but our result (the pentagonal tiling) seems to be the expected optimal partition.

We note the striking resemblance (at least topologically) between our results and the one obtained by Cox and Flikkema (link) in the case of equi-areal partitions which minimize the total perimeter. This similarity was also seen in the 2D computations. As seen here, asymptotically, the optimal 2D spectral partition consists (numerically) of a tiling of regular hexagons. This was proved by T. Hales in the case of the plane equi-areal partitions which minimize the total perimeter.

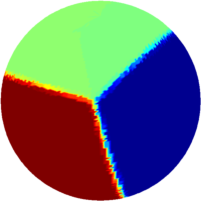
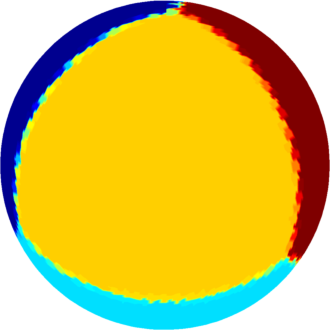
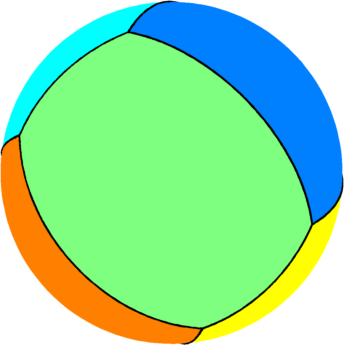
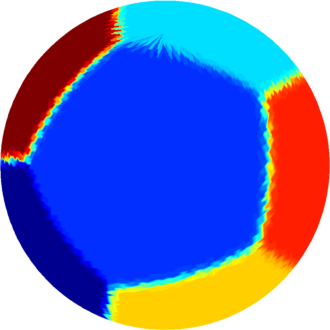
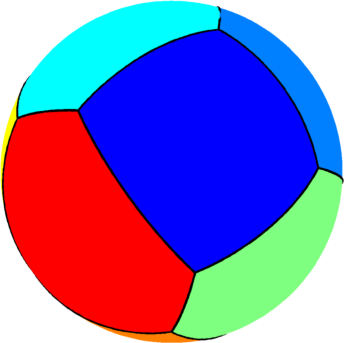
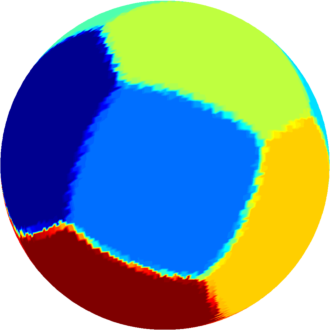
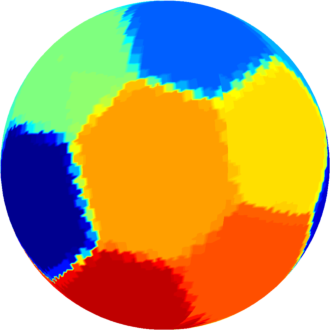
The computations presented below were made using Matlab, and the visualization was made in Matlab using a code based on the package geom3d. The results obtained using a density method are represented on a triangulation of the sphere, using a nearest point interpolation; this is the reason that the boundaries are a bit blurry.

Refined results A glimpse of the density results
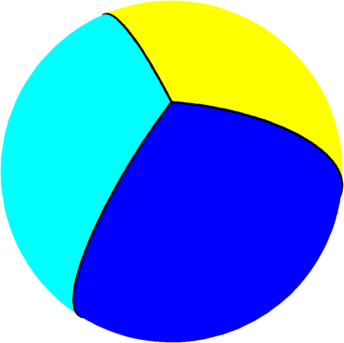
$n=3$ : the optimal partition consists of three $120^\circ$ lens. This fact is not proven theoretically, and is a conjecture proposed by Bishop. The case of the problem $$\min \max_{i=1,2,3} \lambda_1^{LB}(S_i)$$ was solved by B. Helffer, T. Hoffmann-Ostenoff, S. Terracini. They found the same optimal partition.

The optimal value is $45/4$, as the eigenvalue of each slice is $15/4$.
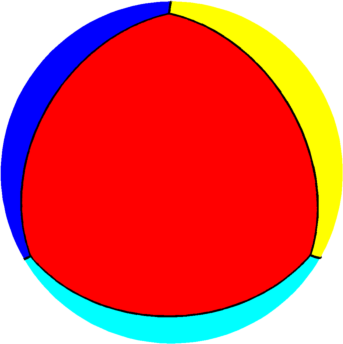
$n=4$ : the optimal partition consists of the tiling generated by a regular tetrahedron inscribed in the sphere.

The optimal energy value is equal to $20.635$ and the corresponding first eigenvalue of the one tetrahedral triangle is equal to $5.1588$. This is the same as the numerical value provided by Ratzkin and Treibergs in this article.

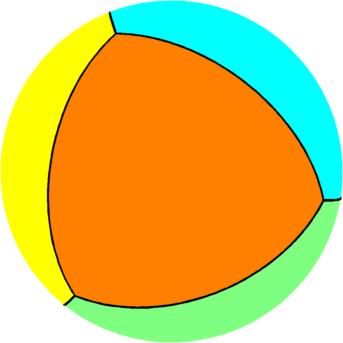
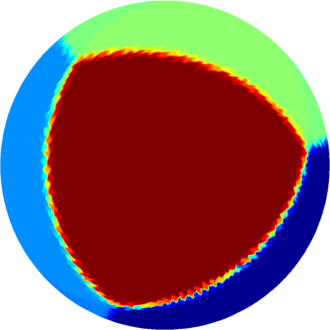
$n=5$ : the optimal partition consists of two equal equilateral triangles joined by three equal rectangles.

The optimal energy value is equal to $34.44$. The eigenvalue of the triangle is $7.26$ and the eigenvalue of the rectangle is $6.57$.
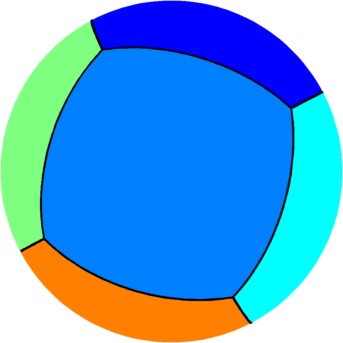
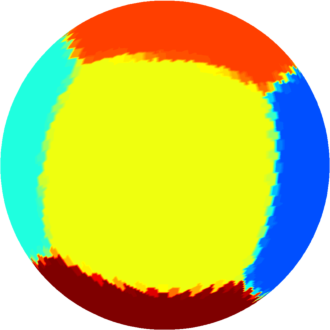
$n=6$ : the optimal partition consists of the tiling generated by a cube inscribed in the sphere.

The optimal energy value is equal to $48.6$ and the corresponding first eigenvalue of one square is equal to $8.10$.
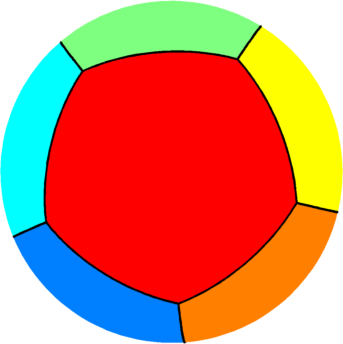
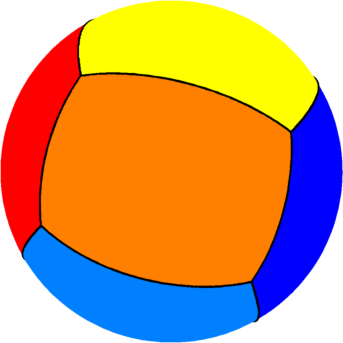
$n=7$ : the optimal partition consists of two equal pentagons joined by five equal rectangles.

The optimal energy value is equal to $69$. The eigenvalue of the pentagon is $8.62$ and the eigenvalue of the rectangle is $10.35$.
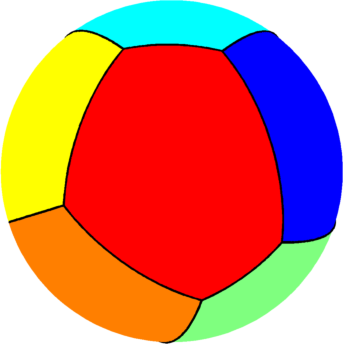
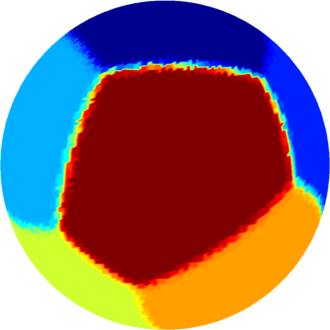
$n=8$ : the optimal partition consists a tiling formed of four pentagons and four quadrilaterals.

The optimal energy value is equal to $91.01$. The eigenvalue of the pentagon is $10.82$ and the eigenvalue of the quadrilateral is $11.93$.
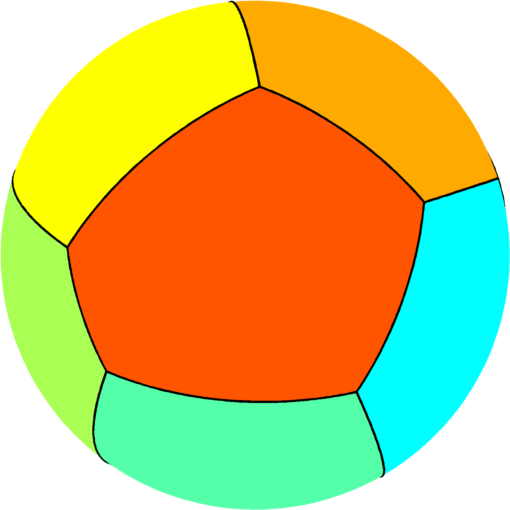
$n=9$ : the optimal partition consists of three equal quadrilaterals joined by six equal pentagons.

The optimal energy value is equal to $115.90$. The eigenvalue of the pentagon is $12.38$ and the eigenvalue of the rectangle is $13.64$.
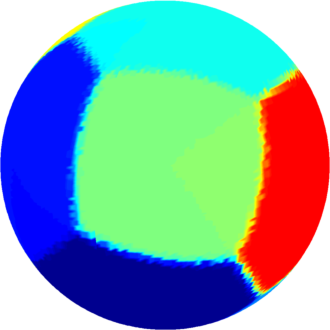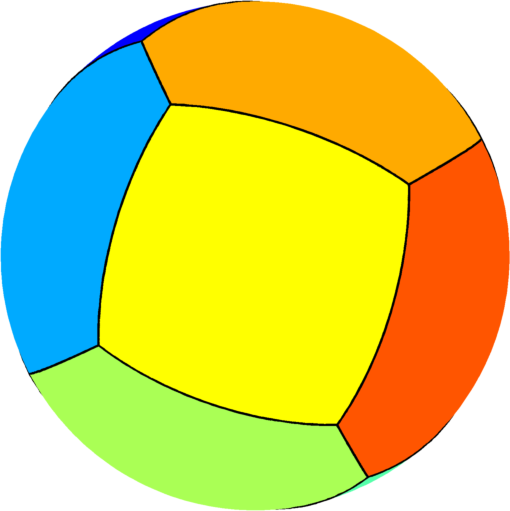
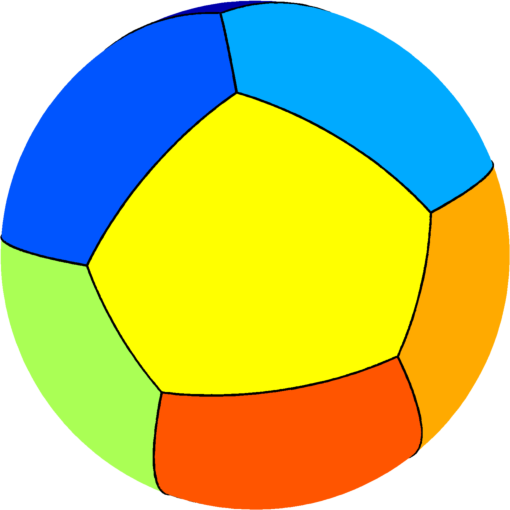
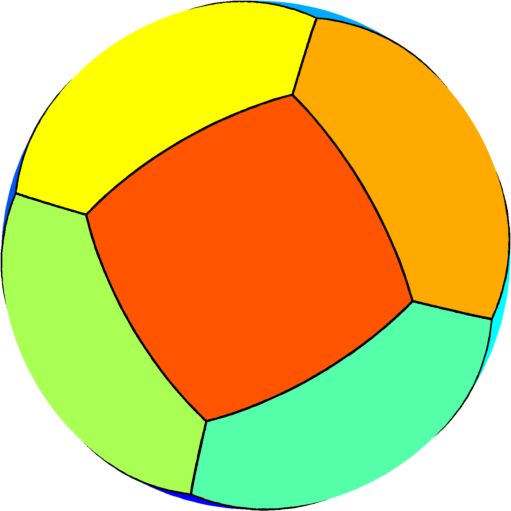
$n=10$ : the optimal partition consists of two equal squares joined by eight equal pentagons.

The optimal energy value is equal to $142.33$. The eigenvalue of the pentagon is $13.95$ and the eigenvalue of the square is $15.85$.
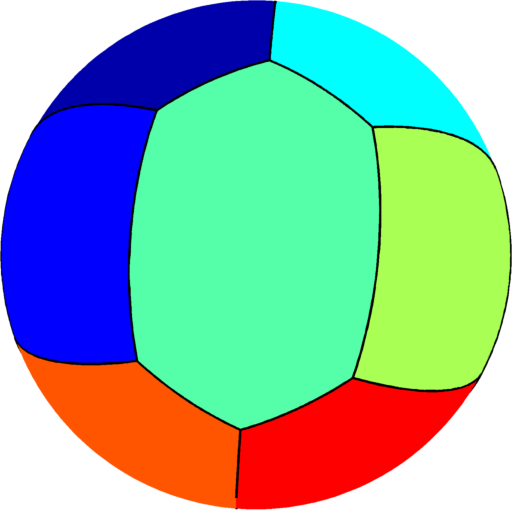
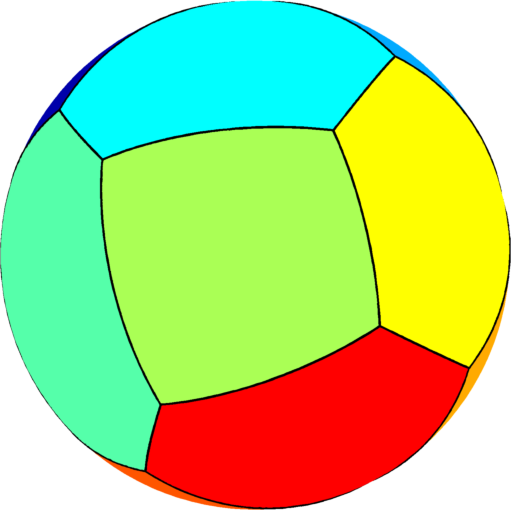
$n=11$ : the optimal partition consists of one hexagon two equal quadrilaterals and eight pentagons of three types.

The optimal energy value is equal to $175.38$. The eigenvalue of the pentagon hexagon is $14.47$, the eigenvalue of the quadrilateral is $17.65$, and the three types of pentagons have eigenvalues in the set $\{15.36,15.77,15.83\}$.
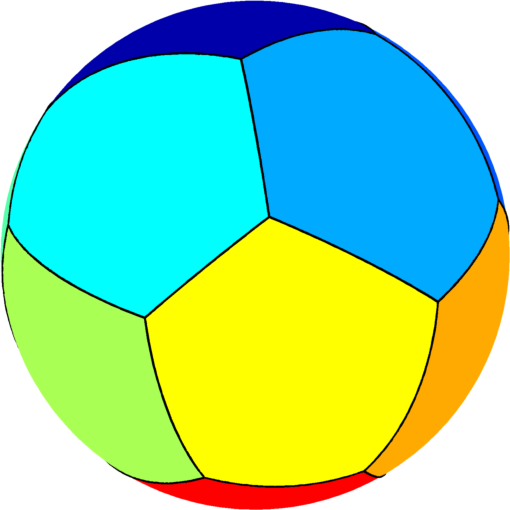
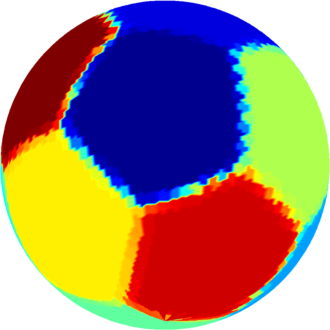
$n=12$ : the optimal partition consists of the tiling of the sphere into $12$ equal pentagons (generated by a dodecahedron).

The optimal energy value is equal to $203.84$ and the corresponding first eigenvalue of one pentagon is equal to $16.99$.
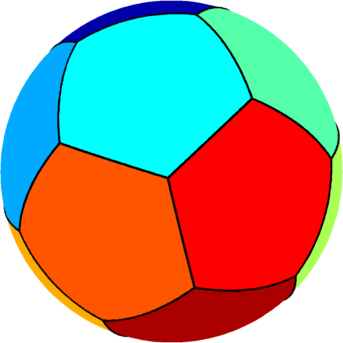
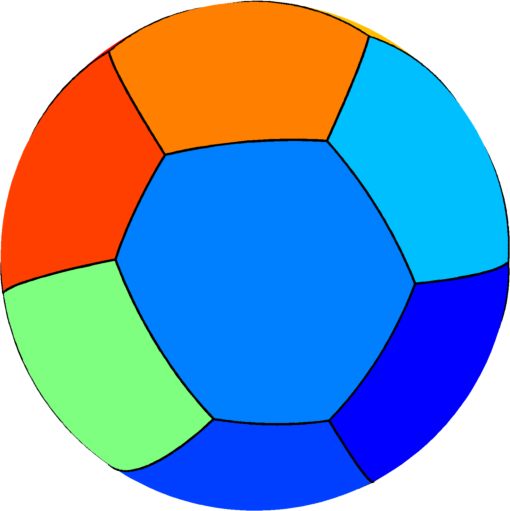
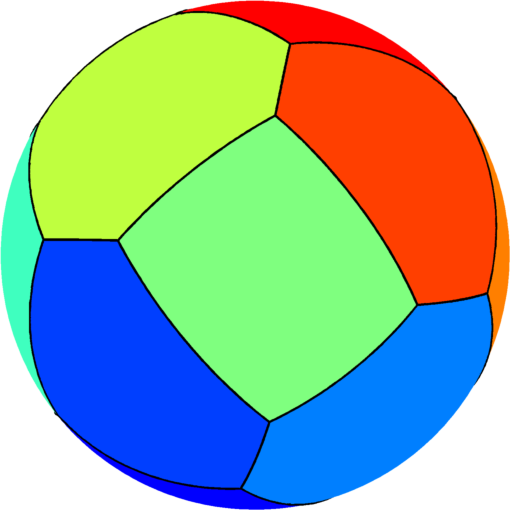
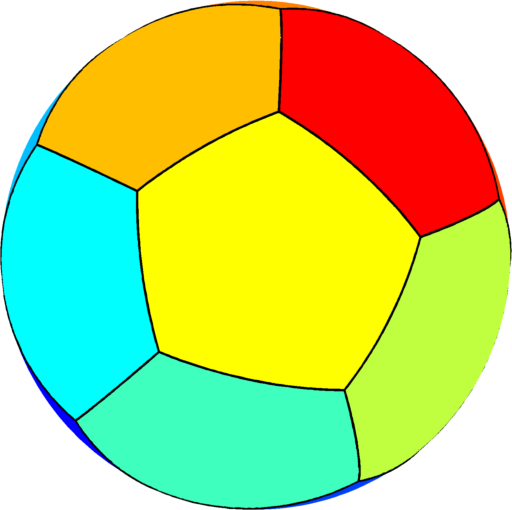
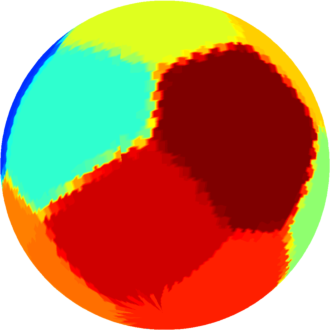
$n=13$ : the optimal partition consists of one rectangle two equal hexagons and ten pentagons of three types.

The optimal energy value is equal to $245.55$.

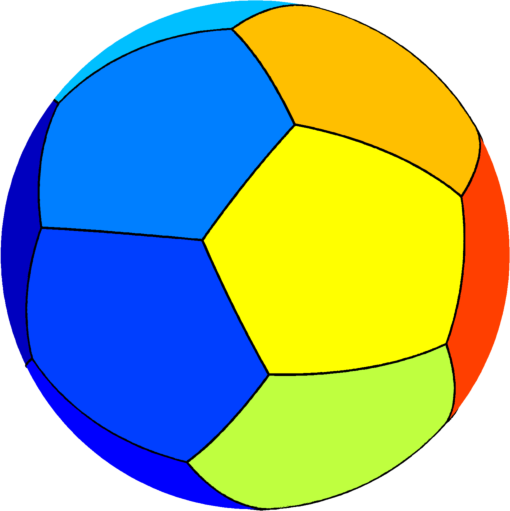
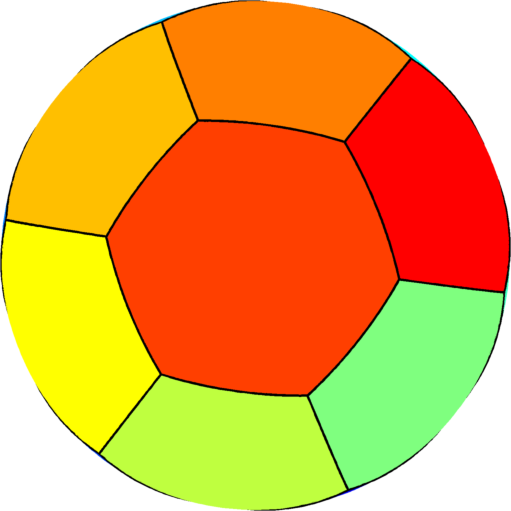
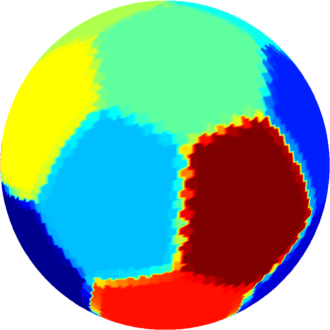
$n=14$ : the optimal partition consists of two equal hexagons joined by $12$ equal pentagons.

The optimal energy value is equal to $283.93$. The eigenvalue of the pentagon is $20.75$ and the eigenvalue of the hexagon is $17.47$.
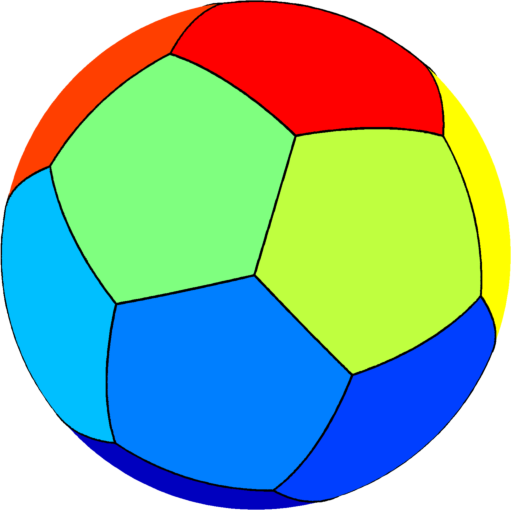
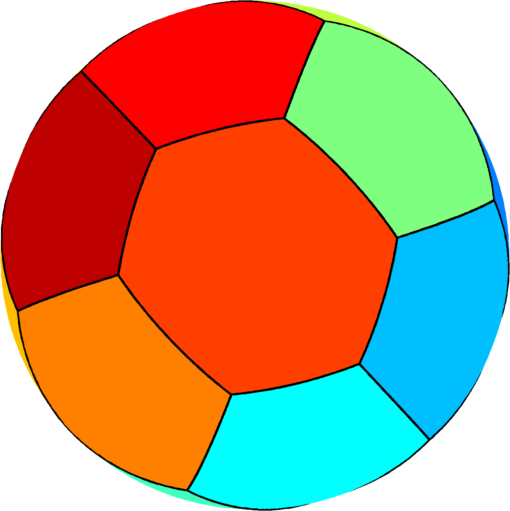
$n=15$ : the optimal partition consists of three equal hexagons joined by $12$ pentagons of two types.

The optimal energy value is equal to $327.21$.

$n=16$ : optimal structure consists of four regular hexagons joined by $12$ equal pentagons.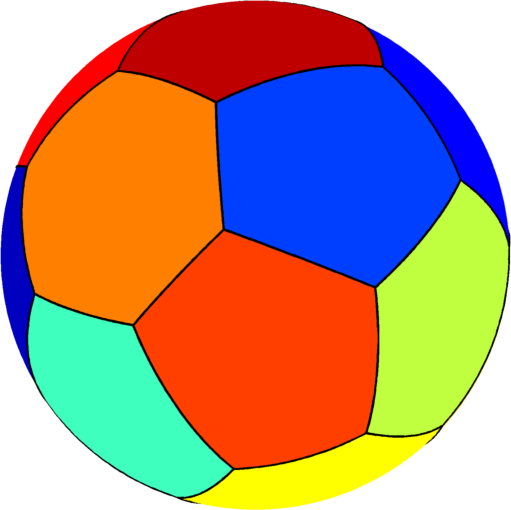
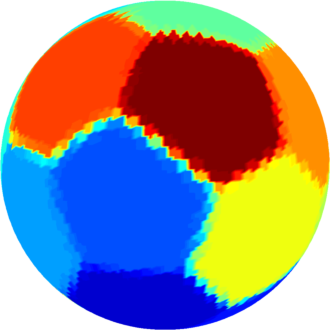$n=17$ : The optimal partition consists of $5$ hexagons and $12$ pentagons. Among the hexagons, four are equal, and there are two pairs and two quadruples of equal pentagons. The optimal computed cost is $423.19$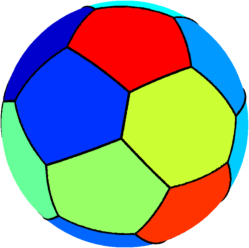
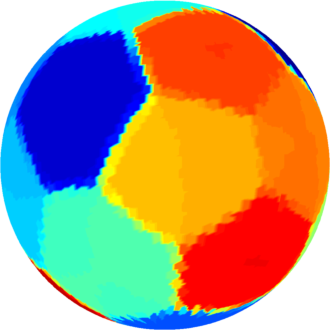$n=18$ : The optimal partition consists of six equal hexagons (with eigenvalue $24.07$) and two groups of six equal pentagons (with eigenvalues $27.28$ and $27.90$). The optimal computed cost is $475.53$
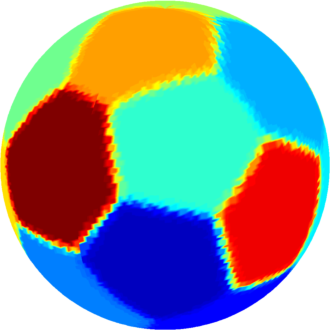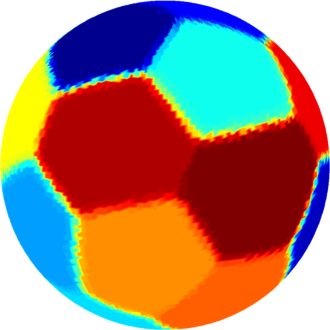
$n=19$ : the optimal partition consists of $7$ hexagons (one plus three pairs of equal hexagons) and $12$ pentagons (six pairs of equal pentagons). The optimal computed cost is $531.00$.
$n=20$ : The optimal partition consists of $8$ hexagons (two groups of four equal hexagons) and $12$ pentagons (one group of four equal pentagons and another group of eight equal pentagons). The optimal computed cost is $586.63$.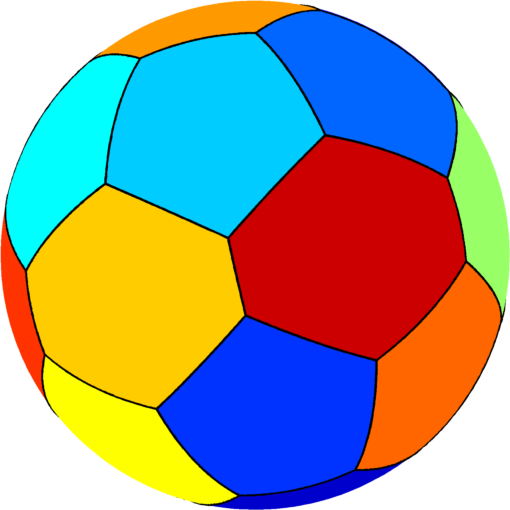
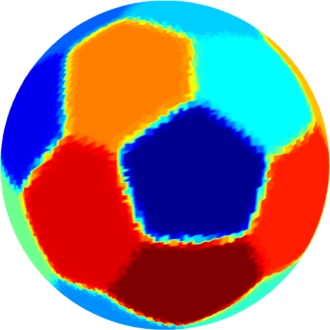$n=21$ : refined results coming soon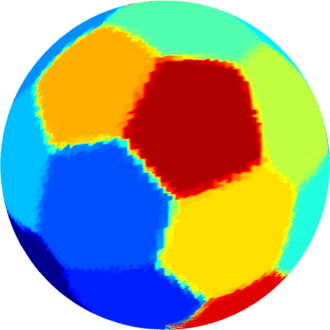
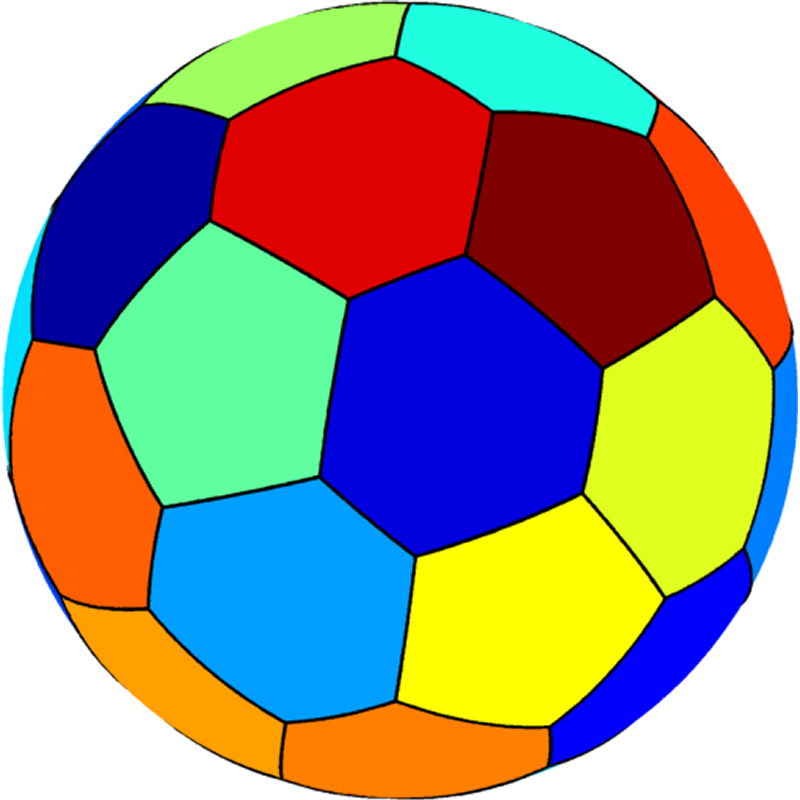
$n=32$ : The optimal tiling has a $C_{60}$ fullerene structure (similar to a soccer ball) consisting of $12$ equal regular pentagons and $20$ equal regular hexagons. The pentagon eigenvalue is equal to $49.34$ and the hexagon eigenvalue is equal to $45.72$. The optimal numerical sum of the eigenvalues is $1506.61$.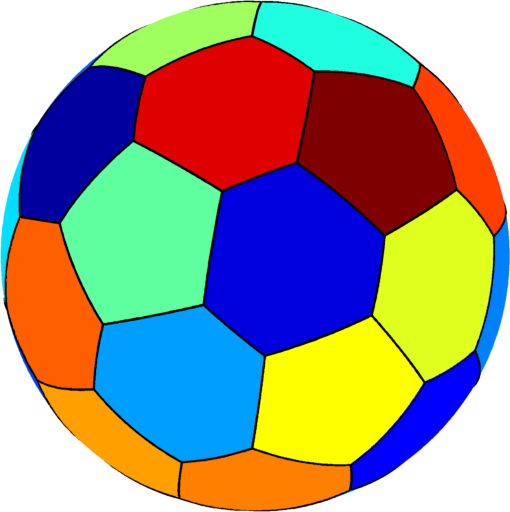

Created: Apr 2015